Дан треугольник ABC. AM и CH – высоты.
Докажите подобие треугольников ABC и MBH.
Другие вопросы по теме Геометрия
Популярные вопросы
- Зробіть будь ласка номер 39(4,5,6) і номер 40(всі) ів...
1 - Укажіть речовину x що відповідає схемі перетворення CO2- x- BaCl2...
2 - 1. Давайте определим причины географических открытий. Как вы думаете,...
1 - Обоснуйте примерами зависимость рек Евразии от рельефа и климата...
2 - Найдите площадь фигуры ограниченной линией и y=0...
2 - Составить сообщение на тему : Православие в Древней Руси ...
3 - какое знаете ( и если не трудно то росписать почему так)...
1 - история слесарного верстака...
1 - 13 B В коробку размером10 см х 10 см х 20 смПЛОТНО уложили кубики...
3 - 1. Paraphrase the following sentences using the speech patterns:...
1
Объяснение:
Дано: ΔАВС;
AM и CH – высоты.
Доказать:
ABC ~ MBH.
Доказательство:
1. Рассмотрим ΔАВМ и ΔНВС - прямоугольные.
∠В - общий.
Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.⇒ ΔАВМ ~ ΔНВС
Запишем отношение сходственных сторон:
2. Рассмотрим ΔABC и ΔMBH.
∠В - общий.
Из п.1 :
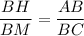 или
или 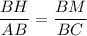
Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны.⇒ ΔABC ~ ΔMBH.