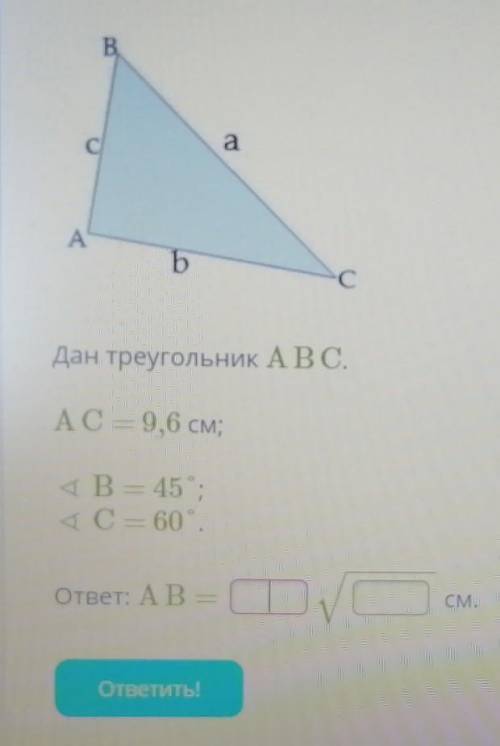
Дан треугольник ABC AC 9,6 угол B 45 угол с 60 AB равно​

Хорошо! Давайте решим этот математический вопрос шаг за шагом.

У нас есть треугольник ABC, где AC = 9,6, угол B = 45°, угол С = 60° и AB равно некоторому значению (это значение нам нужно найти).

Первым шагом в решении этой задачи будет использование закона синусов.
Закон синусов устанавливает соотношение между сторонами и углами треугольника. Он гласит: отношение любой стороны треугольника к синусу противолежащего ей угла равно отношению любой другой стороны к синусу противолежащего угла.

Однако, перед тем, как мы применим закон синусов, нам нужно найти значение стороны AB. Мы можем использовать теорему косинусов для этого.

Теорема косинусов гласит, что квадрат стороны, противолежащей данному углу, равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса данного угла.

Применим теорему косинусов к нашему треугольнику ABC.
Мы ищем значение стороны AB, поэтому в данной формуле сторона AB будет стоять перед квадратом этой стороны.

(AB^2) = (AC^2) + (BC^2) - 2 * AC * BC * cos(B)

У нас есть следующие значения:
AC = 9,6, угол B = 45°, BC (которое нам нужно найти) и угол С = 60°.

Теперь у нас есть все данные для использования теоремы косинусов и нахождения значения стороны AB.

(AB^2) = (9,6^2) + (BC^2) - 2 * 9,6 * BC * cos(45°)

Мы знаем, что cos(45°) = sqrt(2) / 2 (это стандартное значение).

(AB^2) = 92,16 + (BC^2) - 13,44 * BC * (sqrt(2) / 2)

Далее нам нужно упростить это выражение. Для начала, раскроем скобку для умножения:

(AB^2) = 92,16 + (BC^2) - 9,504 * BC * sqrt(2)

Теперь мы можем отбросить степень двойки, так как мы знаем, что стоит знаменатель sqrt(2):

(AB^2) = 92,16 + (BC^2) - 9,504 * BC

Мы получили очень длинное выражение, но не волнуйтесь, мы продолжим его упрощение.

Следующим шагом будет применение закона синусов для нахождения значения стороны BC.

Закон синусов гласит: отношение стороны треугольника к синусу противолежащего угла равно отношению другой стороны к синусу противолежащего другого угла.

В нашем случае, стороной треугольника, которую нам нужно найти, является BC. Противолежащим углом для BC является угол C (60°). Соответственно, мы знаем, что сторона AC равна 9,6. Противолежащим углом для стороны AC является угол B (45°).

Вернемся к формуле закона синусов:

BC / sin(C) = AC / sin(B)

Подставим известные значения:

BC / sin(60°) = 9,6 / sin(45°)

Теперь нам нужно найти значения синусов этих углов. Используя таблицу значений синусов, мы находим:

sin(60°) ≈ 0,866
sin(45°) ≈ 0,707

Заменим эти значения в нашей формуле:

BC / 0,866 = 9,6 / 0,707

Для дальнейшего упрощения этого выражения, мы можем умножить обе стороны на 0,866:

BC = (9,6 / 0,707) * 0,866

После вычислений, мы получим значение стороны BC.

Теперь, имея значение BC, мы можем вернуться к уравнению для AB и решить его:

(AB^2) = 92,16 + (BC^2) - 9,504 * BC

Подставим полученное значение BC и продолжим упрощение выражения.

Итак, с помощью теоремы косинусов и закона синусов, мы можем решить математический вопрос, который был задан.