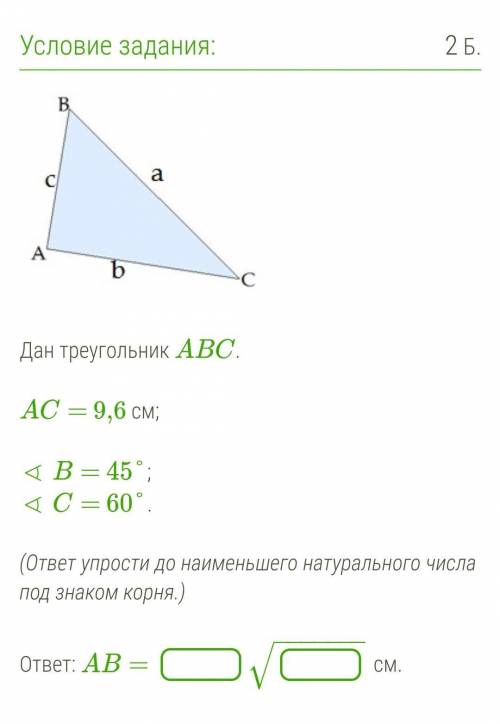
Дан треугольник ABC. AC - 9,6 см
Угол B - 45, угол C - 60.
Остальное на фото ниже
Другие вопросы по теме Геометрия
Популярные вопросы
- Вычислите по действиям 69: 23*12+800: 100= звёздочка это умножение...
1 - Ке частота э/м волны 2мгц найти длину волны...
3 - У=2х-7 2у+3х=0 и это все слева отмечено вот так { ,времени мало....
2 - 1)30/21,52/40,38/30 2)100/90,55/30,48/28 3)68/48,27/24,80/45 4)87/75,26/24,164/80...
3 - Если a(3; 4) и в(-2; 5),то вектор ав имеет...
2 - Ксфере жизни общества относятся: а) президент, правительство, полиция...
3 - Вопрос такой: назовите племена,населявшие в древности территорию казахстана....
1 - Какой зависимостью связаны длины волны,скорость распространения волны,частота...
2 - Название хороводной и пясовой песни и их авторы...
2 - Вядре атома находится 6 протонов и 6 нейтронов. сколько электронов вращаются...
2
по теореме синусов записываем
АС/sin 60=AB/sin 45 sin 60=√3/2 ; sin 45 =√2/2
9,6/(√3/2)=AB/(√2/2)
АВ=(9,6*2)/√3 *(2/√2)= 38,4/√6 = 38,4*√6/(√6*√6)=6,4√6 см
Объяснение:
AB=6,4√6 см
Поскольку угол B равен 45 градусов, а угол C равен 60 градусов, значит, угол A будет равен 180 - 45 - 60 = 75 градусов.
Известно, что сумма углов внутри треугольника равна 180 градусов.
Таким образом, угол А равен 75 градусов.
Теперь, нам необходимо найти сторону AB.
Для этого, мы можем использовать теорему синусов.
В данном случае, мы знаем сторону AC (9,6 см) и угол C (60 градусов).
Теорема синусов формулируется следующим образом:
a/sina = b/sinb = c/sinc,
где a, b и c - стороны треугольника, а A, B и C - соответствующие им углы.
Применяя эту формулу к нашему примеру, мы получим:
AC/sinC = AB/sinA.
Заменим известные значения:
9,6/sin60 = AB/sin75.
Поскольку мы знаем значения синусов 60 и 75 градусов (sin60 = √3/2, sin75 = (√3 + 1)/2√2), мы можем подставить их в формулу.
Для удобства рассмотрим отдельно числитель и знаменатель дробей:
a/b = (√3 + 1)/2√2 = (3 + 2√3 + 1)/(2√2) = (4 + 2√3)/(2√2) = (2 + √3)/√2 = [(2 + √3)/√2] * [(√2)/(√2)] = (2√2 + √6)/2 = √2 + (√6)/2.
Теперь, заменим значения синусов в формуле:
9,6/(√3/2) = AB/[√2 + (√6)/2].
Упростим выражение:
9,6 * (2/√3) = AB/[√2 + (√6)/2].
Здесь, мы можем упростить коэффициент
9,6 * (2/√3) = 19,2/√3.
Теперь, продолжим упрощение:
19,2/√3 ≈ 11,1.
Таким образом, получаем:
AB ≈ 11,1 см.
Ответ: Длина стороны AB примерно равна 11,1 см.