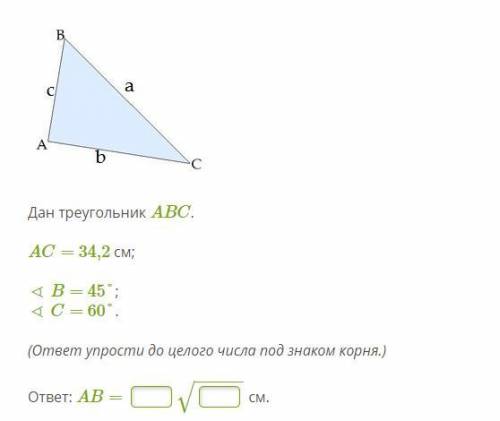
Дан треугольник ABC. AC= 34,2 см;
∢ B= 45°;
∢ C= 60°.
(ответ упрости до целого числа под знаком корня.)
Другие вопросы по теме Геометрия
Популярные вопросы
- Часть А 1. Фольклор – это…1. Устное народное творчество2. Художественная...
1 - Мещанин во дворянстве составить план произведения: 1. Действие...
1 - согревая всё вокруг -деепричастный оборот. какой это вид обстоятельства?...
3 - Является ли Россия мультикультурной страной ?...
1 - Частота этой патологии 1:1000 новорожденных. Клиническая картина:...
3 - Написать отзыв на английском языке на фильм или книгу. по плану...
3 - Найдите наименьшие значение функции на отрезке f(x)=x^2-6x+13,...
2 - Решите неравенство: 4(x-2)-5(x-3) ≤0...
1 - 16ist ein sportart a)leichtathletik b)schrank c)straBe...
3 - Запиши следующие элементы в порядке возрастания их металлических...
3
в треугольнике со сторонами a, b и c и противолежащими углами A, B и C соответственно, отношение синуса каждого угла к его противолежащей стороне равно одной и той же постоянной, которую мы обозначим как k:
sin A / a = sin B / b = sin C / c = k
Здесь даны два угла, B и C, и одна сторона, AC. Мы можем использовать теорему синусов, чтобы найти значение третьей стороны, а затем использовать еще один угол и найденную сторону, чтобы найти оставшиеся значения.
1. Найдем сторону AB:
Используем теорему синусов:
sin B / AB = sin C / AC
sin 45° / AB = sin 60° / 34.2 см
Раскроем синусы и переставим переменные:
AB = (sin 45° * 34.2 см) / sin 60°
Посчитаем значения синусов:
sin 45° ≈ 0.7071
sin 60° ≈ 0.866
Подставим значения в формулу:
AB = (0.7071 * 34.2 см) / 0.866
AB ≈ 28.17 см
2. Теперь найдем угол A:
Используем теорему синусов:
sin A / AB = sin C / AC
sin A / 28.17 см = sin 60° / 34.2 см
Раскроем синусы и переставим переменные:
sin A = (sin 60° * 28.17 см) / 34.2 см
Подставим значения синусов:
sin 60° ≈ 0.866
Посчитаем значение синуса:
sin A ≈ (0.866 * 28.17 см) / 34.2 см
sin A ≈ 0.7115
Теперь найдем угол A, возьмем arcsin от полученного значения:
A ≈ arcsin(0.7115)
A ≈ 45° (возможна погрешность из-за округления)
Итак, мы получили, что угол A ≈ 45°.
3. Найдем угол B:
Угол B у нас уже известен и равен 45°.
4. Найдем угол C:
Угол C = 180° - A - B
C = 180° - 45° - 45°
C = 90°
Итак, у нас получилось, что углы треугольника ABC равны A = 45°, B = 45° и C = 90°.
Теперь можем резюмировать ответ:
В треугольнике ABC со сторонами AC = 34,2 см, AB ≈ 28,17 см и BC = ? (неизвестно), углы B = 45°, C = 90°, A = 45° (возможна погрешность из-за округления).