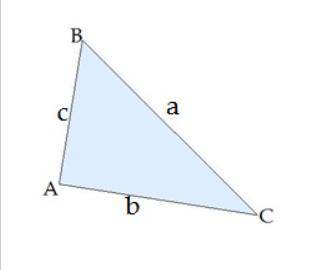
Дан треугольник ABC.

AC= 23,4 см;

∢ B= 60°;
∢ C= 45°.
ответ: AB=

Для решения данной задачи используем теорему синусов.

Теорема синусов утверждает, что в любом треугольнике отношение синуса угла к соответствующей стороне равно отношению синуса противолежащего угла к противолежащей стороне:
sin(A) / a = sin(B) / b = sin(C) / c

Мы можем использовать эту формулу для нахождения стороны AB.

В данном случае известны два угла: ∢ B = 60° и ∢ C = 45°, и одна сторона: AC = 23,4 см.

Шаг 1: Найдем третий угол ∢ A суммируя углы треугольника:
∢ A = 180° - (∢ B + ∢ C)
∢ A = 180° - (60° + 45°)
∢ A = 75°

Шаг 2: Подставим известные значения в формулу теоремы синусов:
sin(∢ A) / a = sin(∢ B) / b

Шаг 3: Рассчитаем значение синуса для каждого угла:

sin(∢ A) = sin(75°)
sin(∢ B) = sin(60°)

Шаг 4: Решим уравнение относительно неизвестной стороны AB:

sin(75°) / AB = sin(60°) / 23,4 см

Для решения этого уравнения нам понадобится применить обратные функции тригонометрии (арксинус). Подставим значения и решим:

AB = (sin(75°) / sin(60°)) * 23,4 см