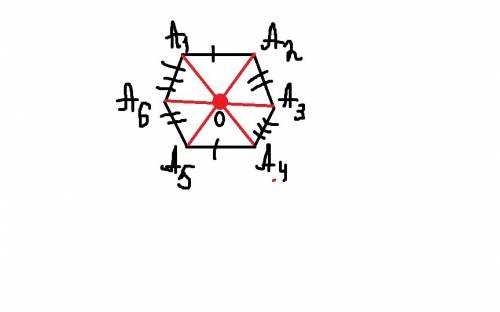
Дан шестиугольник a1 a2 a3 a4 a5 a6. его стороны a1 a2 и a4 a5, a2 a3 и a5 a6,a3 a4 и a6 a1 попарно равны и паралельны используя центральную симметрию, докажите , что диагонали a1 a4, a2 a5, a3 a6 данного шестиугольника пересекаются в одной точке
Ответы
Все полученные треугольники равны (по стороне и двум углам при ней). Это означает, что диагонали в точке их пересечения делятся пополам. Поэтому у фигуры есть центр симметрии. И все диагонали, соединяющие центрально симметричные вершины проходят через центр симметрии и делятся им пополам.
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Кліматичні пояси в яких знаходиться Євразія. ( 7 клас)...
2 - найти ответ 26 · (96 – 96) + 48 : (29 + 19) + 32 : (84 – 83) =...
2 - Роки князювання Василька Романовича...
2 - 35 жетонів, занумерованих числами від 1 до 35, виймають один. Яка...
3 - 2+2= я дурак и кто решит, не за что)...
3 - визначте масу натрію якщо при взаємодії його з водою утворилося 112...
3 - Знайдіть сьомий член і суму двадцяти перших членів арифметичної прогресії...
1 - Побудуйте в одній системі координат графіки функцій у = 0,5 х і у...
3 - Прислівник виконує роль присудка в реченні А Блідий ранок несміливо...
3 - Может ли человечество существовать в отрыве от природы - на пример,...
2