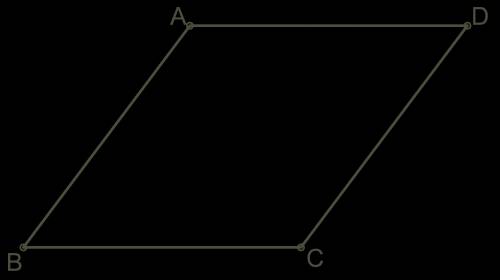
Дан ромб ABCD. Выбери одно самое подходящее название данных векторов:

а. AD−→− и DA−→− —

противоположные
ни одно название не подходит
сонаправленные
равные
противоположно направленные

b. BC−→− и AD−→− —

сонаправленные, но не равные
противоположно направленные
ни одно название не подходит
противоположные
равные

c. CB−→− и AD−→− —

противоположно направленные
сонаправленные
равные
ни одно название не подходит
противоположные

d. AD−→− и CD−→− —

ни одно название не подходит
сонаправленные
противоположно направленные
противоположные
равные

Привет! Давай разберем варианты по очереди и найдем подходящие названия векторов.

а. AD−→− и DA−→− —
В данном случае векторы AD−→− и DA−→− идут из одной точки A в другую точку D, но имеют разные направления (один вправо, другой влево). По определению, противоположные векторы представляют собой векторы одинаковой длины, но с противоположными направлениями. В данном случае, векторы AD−→− и DA−→− не являются противоположными, так как они имеют разные направления.

Ответ: ни одно название не подходит.

b. BC−→− и AD−→− —
В данном случае векторы BC−→− и AD−→− идут из точки B в точку C и из точки A в точку D соответственно. Они идут в разных направлениях (один вверх, другой вправо), поэтому не могут быть сонаправленными. Также они имеют разные длины, поэтому не могут быть равными. Но направления векторов BC−→− и AD−→− противоположны (один идет вверх, другой вниз), поэтому можно сказать, что они противоположно направленные.

Ответ: противоположно направленные.

c. CB−→− и AD−→− —
В данном случае вектор CB−→− идет из точки C в точку B, а вектор AD−→− идет из точки A в точку D. Они идут в разных направлениях (один влево, другой вправо), поэтому не могут быть сонаправленными. Но направления векторов CB−→− и AD−→− противоположны (один идет влево, другой вправо), поэтому можно сказать, что они противоположно направленные.

Ответ: противоположно направленные.

d. AD−→− и CD−→− —
В данном случае векторы AD−→− и CD−→− идут из точки A в точку D и из точки C в точку D соответственно. Они идут в разных направлениях (один вправо, другой влево), поэтому не могут быть сонаправленными. Они также имеют разные длины, поэтому не могут быть равными. Также их направления противоположны (один идет вправо, другой влево), поэтому можно сказать, что они противоположно направленные.

Ответ: противоположно направленные.

Таким образом, подходящие названия векторов будут следующими:
а. ни одно название не подходит
b. противоположно направленные
c. противоположно направленные
d. противоположно направленные