Дан ромб ABCD. Диагонали ромба- АС=48см; BD=14см
найдите сторону ромба.
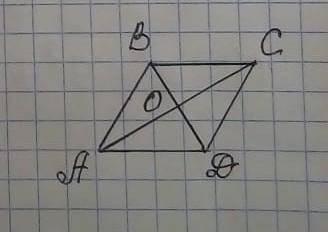
Другие вопросы по теме Геометрия
Популярные вопросы
- Однородные сказуемое в предложение гуси и лебеди (=), (=), (=) (=)-однородное...
1 - Решить : 1): в магазин 180кг картофеля.в 1 день продали 5/9 всего...
3 - Составь выражения и найди их значения: из суммы чисел 381 и 619 вычти...
2 - Как оформить реакцию! ? есть цепочка: al — al2o3 — al 2(so4)3 — al(oh)3...
3 - Поставити всі дієслова у past tense 1. as the boy is walking along,...
3 - Начерти отрезки длиной 9 см и 1 дм. сравни...
1 - Составить 6 вопросов и 6 ответов на тему олимпийские игры, на...
2 - Св ! обе решить тремя вывести последовательность чисел на экран 12,...
1 - На каких материках живут зайцеобразные, ластоногие, китообразные,...
2 - Сколько уксусноэтилового эфира получится при действии 100 г уксусной...
1
Свойства ромба:
1. В ромбе все стороны равны.
2. Диагонали ромба пересекаются под прямым углом и делят его на четыре равных треугольника.
Дано: AC = 48 см и BD = 14 см.
Сначала, найдем длину одной стороны ромба, обозначим ее через x.
Поскольку диагонали ромба пересекаются под прямым углом и делят его на четыре равных треугольника, получим, что высота треугольника ABD равна половине диагонали BD, то есть h = BD / 2 = 14 / 2 = 7 см.
Используя теорему Пифагора, найдем длину стороны ромба:
AB^2 = AD^2 + BD^2
AB^2 = (AC/2)^2 + BD^2
AB^2 = (48/2)^2 + 14^2
AB^2 = 24^2 + 14^2
AB^2 = 576 + 196
AB^2 = 772
AB = √772 ≈ 27.8 см
Ответ: Сторона ромба приблизительно равна 27.8 см.