1. Геометрия
  2. Дан равнобедренный треугольник

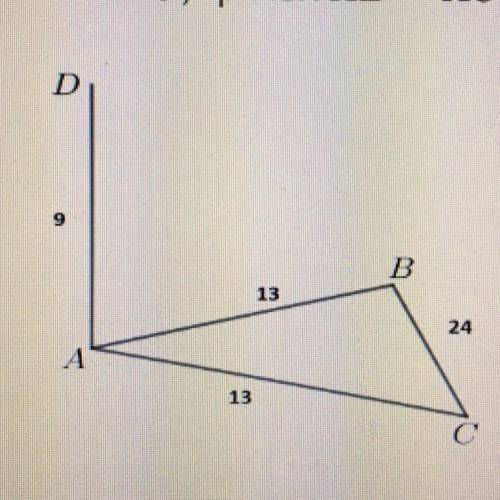
Дан равнобедренный треугольник ABC, причем AB = AC = 13, а ВС = 24. В точке А построен перпендикуляр к плоскости треугольника так, что AD = 9.
Найдите расстояние от точек A и D до прямой BC. В ответ запишите квадраты
соответствующих величин.


Дан равнобедренный треугольник ABC, причем AB = AC = 13, а ВС = 24. В точке А построен перпендикуляр

lizabatyshkina lizabatyshkina    2   14.12.2020 23:45    32

Ответы
znani5 znani5  13.01.2021 23:47

AH2=25; DH2=106

Объяснение:

Расстояние от A до BC (возьмем AH-перпендикуляр) - высота, медиана и биссектриса соответствующего треугольника ABC. Мы можем его найти по теореме Пифагора: AH2=AC2-CH2

CH= 1/2 BC = 12

AH2=169-144=25

Расстояние от D до BC (DH) - гипотенуза треугольника ADH

DH2=AH2+AD2

DH2=25+81=106

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
alsuu00 alsuu00  21.06.2019 08:10
Основание равнобедренной трапеции 3 и 5, диагонали взаимно перпендикулярны. найдите высоту трапеции....
goodman91 goodman91  21.06.2019 08:10
1)s прямоугольника abc=30(градусов),катет ас=5.найти гипотенузу ав 2)в прямоугольном авс (∠с=90(градусов)) ас=30,медиана см=25.найти вс...
oldespower oldespower  21.06.2019 08:10
47 ! докажите, что если основание и медиана,проведенная к боковой стороне одного равнобедренного треугольника, равны основанию и медиане, проведенной к боковой стороне другого...
alinavinokutov alinavinokutov  21.06.2019 08:10
Один из углов прямоугольной трапеции равен 135 градусов, средняя линия - 21 см, а основания относятся как 5 : 2. найдите меньшую боковую сторону трапеции....
Alice26the03time2004 Alice26the03time2004  21.06.2019 08:10
С, : дано: dabc-пирамида треугольник авс-равнобедренный ас=ав=10, вс=12. каждый из двугранных углов при основании равен 45 найти объем...
Sabaydin Sabaydin  21.06.2019 08:10
Решите треугольник по указанным данным : b=2,c=3,угол а=40градусов...
milinamonid milinamonid  21.06.2019 08:10
Катеты прямоугольного треугольника равны 15 и 20 сайдите их проекцию на гепотинузу...
DimaKravshenco DimaKravshenco  21.06.2019 08:10
Впрямоугольнике abcd диагонали ac=8*√3см и образует с большей стороной прямоугольника угол 30°. найдите стороны прямоугольника...
АльпакаКайа АльпакаКайа  21.06.2019 08:10
Найдите углы треугольника авс если угол а : угол в : угол с равно 1: 2: 3...
emilio1324 emilio1324  21.06.2019 08:10
Укажите номера верных утверждений: 1) любые два равносторонних треугольника подобны. 2) прямоугольном треугольнике все углы равны. 3)диагонали параллелограмма перпендикулярны....

Популярные вопросы