Дан прямоугольный треугольник авс угол с =90 ас =30 ав=34 св =16 найти расстояние между центром описанной и вписанной окружности?

Question

Геометрия: Дан прямоугольный треугольник авс угол с =90 ас =30 ав=34 св =16 найти расстояние между центром описанной и вписанной окружности?

helpmeplsaaa · Answer

Радиус вписанной окружности считается по известной формуле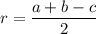 $r=\dfrac{a+b-c}{2}$ , а радиус описанной окружности: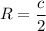 $R=\dfrac{c}{2}$

Вычислим радиусы описанной и вписанной окружностей.

$r=OD=OE=OF=\dfrac{BC+AC-AB}{2}=\dfrac{16+30-34}{2}=6\\ \\ R=BO_1=AO_1=\dfrac{AB}{2}=\dfrac{34}{2}=17$

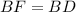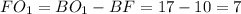
Далее BF=BD как отрезки касательных к окружности, проведенные из одной точки. Следовательно, BD=BF=BC-CD=16-6=10 , тогда длина отрезка FO_1=BO_1-BF=17-10=7

Из прямоугольного треугольника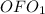 OFO_1 найдем расстояние между центром описанной и вписанной окружности

$OO_1=\sqrt{FO_1+OF^2}=\sqrt{7^2+6^2}=\sqrt{85}$

ответ: $\sqrt{85}$

Дан прямоугольный треугольник авс угол с =90 ас =30 ав=34 св =16 найти расстояние между центром опис

Дан прямоугольный треугольник авс угол с =90 ас =30 ав=34 св =16 найти расстояние между центром описанной и вписанной окружности?

Популярные вопросы