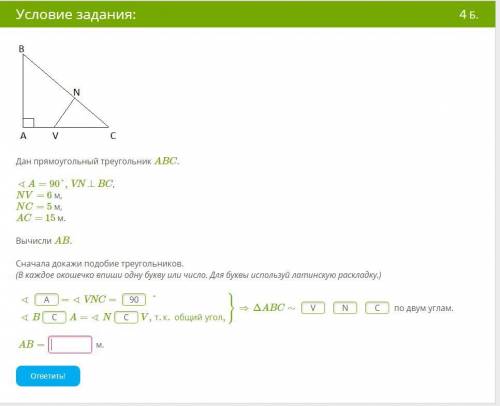
Дан прямоугольный треугольник ABC. ∢A=90°,VN⊥BC,
NV= 6 м,
NC= 5 м,
AC= 15 м.
Вычисли AB.
Сначала докажи подобие треугольников.
(В каждое окошечко впиши одну букву или число. Для буквы используй латинскую раскладку.)
∢
=∢VNC=
°∢B
A=∢N
V,т.к. общий угол,}⇒ΔABC∼
по двум углам.
Другие вопросы по теме Геометрия
Популярные вопросы
- решите уравнение в течении 5 минут...
2 - Тило рухаеться зи швидкистю 5км/год протянем 3 годин знайте шлях пройденном тилом...
2 - Функция задана формулой у=4х-30...
3 - 4. «Язык является не только языком межнационального международного общения, но...
1 - Внутрішня будова річкового рака!...
2 - Социальный слой служащих в статусном отношении обычно считается более высоким,...
3 - Выберите наиболее значимую характеристику предприятия производственно техническое...
3 - 4. Дайте полное описание химического элемента по названию и количеству фундаментальных...
1 - Знайти похідну функції у=5-x2...
2 - Обращайте от данных прилагательных существительные по модели прил. + - ость. Мудрый...
3
Шаг 1. Доказательство подобия треугольников:
Мы знаем, что угол <∢A равен 90° (прямой угол). Также угол ∢
VNC равен 90° (так как VN ⊥ BC). Таким образом, угол ∢
VNС равен ∢A.
Мы также знаем, что угол ∢
A равен углу ∢NVC, так как они являются соответственными углами при параллельных прямых VN и BC.
Из этих двух фактов следует, что треугольники ΔABC и ΔVNC подобны по двум углам.
Шаг 2. Вычисление длины AB:
Мы знаем, что отношение длины сторон подобных треугольников равно. Таким образом, мы можем записать следующее отношение:
AB / AC = VN / NC
Подставляя известные значения, получим:
AB / 15 = 6 / 5
Далее, можно решить эту пропорцию относительно AB:
AB = (6 / 5) * 15 = 18 м
Таким образом, длина стороны AB равна 18 метрам.