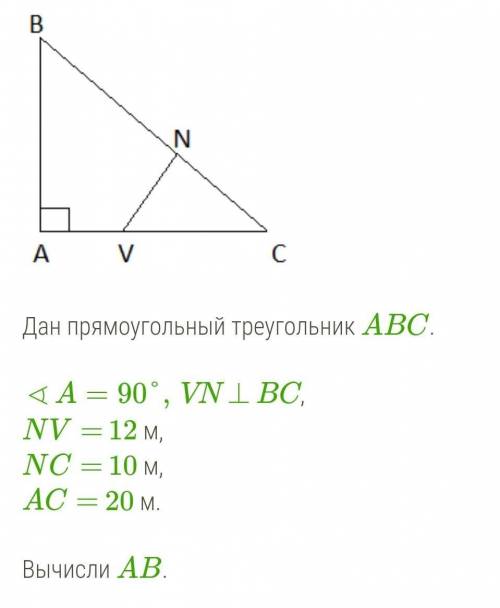
Дан прямоугольный треугольник ABC.
∢A=90°,VN⊥BC,
NV= 12 м,
NC= 10 м,
AC= 20 м.
Вычисли AB.
Сначала докажи подобие треугольников.
(В каждое окошечко впиши одну букву или число. Для буквы используй латинскую раскладку.)
∢BA=∢NV,т.к. общий угол,∢A=∢VC=°⎫⎭⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⇒ΔAC∼V по двум углам.
AB= м.
Другие вопросы по теме Геометрия
Популярные вопросы
- ,решить работу по английскому языку. Заранее...
2 - 11.Не виділяється комами одиничний дієприслівник у реченні (розділові...
3 - 2) Чью жизнь в повести «Тарас Бульба» меняет вспыхнувшее чувство?...
1 - Анализ эпизодов и характеристика героев рассказа И.С. Тургенева...
3 - Task 1. put the verbs in the bracket in a correct passive form....
3 - Що означають такі записи: О, ЗО, , Ci, 5CI, MgO, K,0, 2NO?...
3 - Рассчитайте необходимое количество основных рабочих на участке...
1 - хелп 1 расставить слова в текст 2 перевести текст 3 перевести текст...
1 - Два позитивних заряди 1·10 в степені -9Кл і 2·10 в степені -9Кл...
2 - найдите значение выражения /-3/7/+/-1/14/; /-5/9/*/3/5/...
3
Теперь, используя подобие треугольников ΔACB и ΔNVC, мы можем написать отношение длин сторон.
AB/VC = AC/NV
Мы знаем, что AC = 20 м и NV = 12 м, поэтому мы можем подставить эти значения в уравнение:
AB/VC = 20/12
Теперь нам нужно выразить VC через известные значения. Мы знаем, что NC = 10 м, поэтому VC = NC - NV = 10 - 12 = -2 метра. Отрицательное значение означает, что VC направлен в противоположную сторону, поэтому мы можем взять его абсолютное значение:
AB/|-2| = 20/12
AB/2 = 20/12
Теперь найдите AB, умножив обе стороны уравнения на 2:
AB = (20/12) * 2 = 40/12 = 10/3 м
Ответ: AB = 10/3 метра.