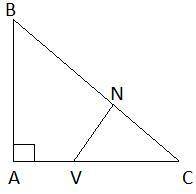
Дан прямоугольный треугольник ABC.
∢A=90°,VN⊥BC,
NV= 10 м,
NC= 8 м,
AC= 16 м.
Вычисли AB.
Сначала докажи подобие треугольников.
(В каждое окошечко впиши одну букву или число. Для буквы используй латинскую раскладку.)
∢B __ A=∢N __ V,т.к. общий угол,
∢ __ =∢VNC= __ ° }⇒ΔABC по двум углам.
∼ __ __ __
AB= __ м.
Другие вопросы по теме Геометрия
Популярные вопросы
- Ставится ли запятая между совершенным и несовершенным деепричастиями? например,...
1 - На дне сосуда, заполненного водой, находится точечный источник света. если...
3 - Взаимодействие этилена с бромом является реакцией: 1 замещения, экзотермической...
1 - Враствор хлорида меди опустили железный гвоздь. эта реакция: 1 замещения,...
1 - Найти все решения неравенства значений чисел: √(x+2)+модуль x-2 модуль ≤...
3 - F(x)=7/2x+5 p.s (2x+5) под корнем, найдите все первообразные функции...
1 - Напишите подалуйста горение альфа-аминопропановой кислоты. и что получится?...
3 - Представьте одночлен а^3bc^4 в виде произведения двух одночленов 4-ой степени...
2 - Распределить слова по столбикам [ i ] [ e ] [ ai ] [ эu ] [ æ ] [ ei ] слова:...
1 - Морфемный разбор слова отрядморфемный разбор слов отряд берега рюкзаки разожгли...
3
Из условия задачи, мы знаем, что ∢A=90°, а также VN⊥BC, что означает, что отрезок VN является высотой, проведенной из вершины N. Таким образом, треугольник ABC является прямоугольным треугольником с прямым углом при вершине A.
Теперь давайте посмотрим на треугольник AНV. У нас есть NV=10 м и NC=8 м. По теореме Пифагора мы можем найти длину AC:
AC² = NV² + NC²
AC² = 10² + 8²
AC² = 100 + 64
AC² = 164
AC = √164
AC ≈ 12.80624 м
Теперь у нас есть длины двух сторон треугольника ANC: AC≈12.80624 м и NC=8 м.
Мы также знаем, что треугольник ABC подобен треугольнику ANC по двум углам. Тем самым, поскольку треугольники подобны, то и отношения длин соответствующих сторон должны быть равны:
AB/AC = BC/NC
Заменяем известные значения:
AB/12.80624 м = BC/8 м
Теперь нам нужно найти длину BC. Воспользуемся теоремой Пифагора:
BC² = AC² - AB²
BC² = (12.80624 м)² - AB²
Теперь мы можем решить эту формулу относительно AB:
AB² = (12.80624 м)² - BC²
AB² = (12.80624 м)² - (BC/8 м)²
AB² = 164 - (BC/8 м)²
Теперь вернемся к отношению сторон AB/AC = BC/NC:
AB/12.80624 м = BC/8 м
Мы можем заменить BC/NC на AB/AC и решить это уравнение относительно AB:
AB/12.80624 м = AB/AC
AB/12.80624 м = AB/(12.80624 м)
Теперь мы можем сделать уравнение:
AB/12.80624 м = AB/(12.80624 м)
Мы можем умножить оба выражения на 12.80624 м:
AB = AB
Таким образом, мы получаем AB=AB.
Это означает, что длина стороны AB может быть любой, поэтому мы не можем однозначно найти ее.
Ответ: длина стороны AB может быть любой.