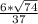Дан прямоугольный параллепипед ABCDA1B1C1D1, AB=5 см, AD=7 см, AA1=12 см. Найдите угол между: 1) прямой DC1 и плоскостью A1B1C1;
2) прямой B1D и плоскостью ABC.
Фото чертежа ниже
, дайте ответ в тетради или тут, но только на русском и чтобы было понятно
Популярные вопросы
- Прочитай по ломаной линии проходящей вдоль клеток, пословицу. при этом...
3 - Морфологический разбор слова первое и фанетический разбор слова моей...
3 - Хозяйка купила 3 ко груш а яблок на 6 кг больше.во сколько раз больше...
1 - Орган в ведении которого находится учет молодежи подлежащий призыву...
1 - Описать как разобрать предложение по по членом...
1 - Суравнениями 29x+67x=30720 50y-28y=832 6z-z+18z=43 2n+7n-12=69...
2 - Величины , выразив в сантиметрах : две пятые дм...
2 - Периметр треугольнтка 89 см с периметр прямоугольника в 3 раза больше.на...
2 - Можно ли так записать программу? var a,a1,a2,a3,a4: integer; begin writeln(...
2 - Раздели слова на слоги. составь звуковую модель первого слога каждого...
2
Объяснение:
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
1) прямая DC1 и плоскость A1B1C1
DD1 ⊥ (A1B1C1) ⇒ DD1 ⊥ D1C1 ⇒ D1C1 - проекция прямой DC1 на плоскость A1B1C1, а ∠DС1D1 - искомый угол.
Рассмотрим ΔDС1D1 (∠D1=90°):
D1C=A1B1=AB=5
DD1=AA1=12
tg ∠DС1D1 = D1D1/C1D1 = 12/5
∠DС1D1 = arctg (12/5)
2) прямая B1D и плоскость ABC
BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD ⇒ BD - проекция прямой B1D на плоскость ABC, а ∠B1DB- искомый угол.
Рассмотрим ΔB1DB (∠B=90°):
BB1=AA1=12
BD найдём из прямоугольного ΔABD(∠A=90°) по т.Пифагора:
BD² =AB²+AD²=25+49=74
tg ∠B1DB=BB1/BD=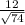 =
=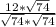 =
= 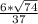
∠B1DB= arctg