Дан прямоугольный параллелепипед ABCDA1B1C1D1 . На ребре АА1 отмечена точка F таким образом, что А1F : FA=3:4. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки F, B1, C1, если ВС 4, АВ 2√7, АА1 14

32 ед².

Объяснение:

Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед.

F∈AA₁, A₁F:FA = 3:4

BC = 4; AB = 2√7; AA₁=14.

Через точки F, B₁,C₁ проходит сечение.

Найти: площадь сечения.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.Противоположные грани параллелепипеда параллельны.

⇒ сечение FB₁C₁C - прямоугольник.

Площадь прямоугольника равна произведению смежный сторон.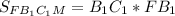

⇒

1. Пусть А₁F = 3x, тогда AF = 4x, а АА₁ = 7х = 14

7х = 14 ⇒ х = 2

Тогда A₁F = 3x = 6

2. Рассмотрим ΔFA₁B₁ - прямоугольный.

A₁F = 6; A₁B₁ = AB = 2√7;

По теореме Пифагора найдем FB₁:

Теперь найдем площадь сечения:

(ед.²)