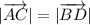Дан прямоугольник abcd доказать что |ab+ad|=|ab-ad| это вектора
Другие вопросы по теме Геометрия
Популярные вопросы
- Напишите 2 предложение слово энциклопедия(в научном стиле речи)...
1 - Выполните морфологический разбор глаголов: ловить , относило ,...
3 - Интерактивная работа в тетради Деление и вычитание дробей...
3 - вычислите кокон количество требуется для обращения спирта массы...
3 - Перечислите кровеносные сосуды животных ?...
1 - 3√81a\6b\2c\4 Математика решить пример...
1 - 25 Гумевасты эпохи Возрождения 1) проявляди дубокий интерес к...
3 - Первоклассникам приготовили для новогодних подарков 87 игрушек...
3 - В магазине игрушек в подарок были куплены три одинаковые игрушки....
3 - Would it be all right if they (come) round at four? Укажите правильный...
3
Векторы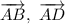 - перпендикулярны, то их скалярное произведение равно 0, то есть
- перпендикулярны, то их скалярное произведение равно 0, то есть 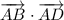
Значит
Следовательно,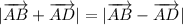 или это
или это