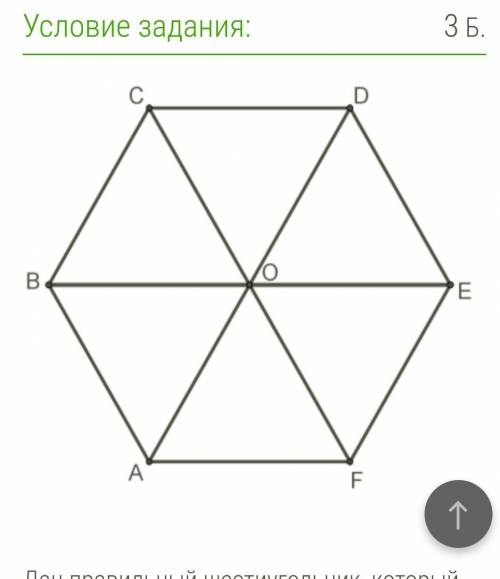
Дан правильный шестиугольник, который состоит из шести правильных треугольников, сторона которых равна 42 см. Определи скалярное произведение данных векторов:
1. AB−→−⋅AD−→−=
;
2. OF−→⋅OA−→−=
;
3. CB−→−⋅CD−→−=
Другие вопросы по теме Геометрия
Популярные вопросы
- В равнобедренном тупоугольном треугольнике АВС с основанием АС проведены биссектриса...
1 - Точка М лежит на прямой АВ. Найдите длину отрезка АМ если АВ=16 и ВМ=3АМ...
1 - Что токое револьвер в микроскопе?...
2 - Рабочий, работая по 4 часа в день, выполняет работу за 12 дней. За сколько дней...
2 - Решите -13×6+53 По действиям...
1 - Что относится к источникам информации...
2 - нужна только правильный ответ дайте Кто ответит на вопрос тот получить все ...
2 - Опытное поле разбили на два участка. Площадь первого участка a га, а второго — b...
2 - Help me! 1.Find the incorrect sentences. a) Oh, no! It rains again! b) Where do...
3 - Мына тужырымдамалардын кайсысы дурыс? 1)ен улкен натурал сан жок 2)кез келген натурал...
1
Прежде всего, вычислим длину векторов AB−→ и AD−→. Так как стороны треугольника равны 42 см, то длина вектора AB−→ равна длине стороны треугольника, то есть 42 см.
Таким же образом, длина вектора AD−→ также равна 42 см.
Для определения косинуса угла между векторами AB−→ и AD−→ воспользуемся формулой косинуса:
cos(θ) = (AB−→⋅AD−→) / (|AB−→|⋅|AD−→|),
где AB−→⋅AD−→ обозначает скалярное произведение, |AB−→| и |AD−→| обозначают длины этих векторов.
Сначала найдем скалярное произведение AB−→⋅AD−→:
AB−→⋅AD−→ = |AB−→|⋅|AD−→|⋅cos(θ).
Так как угол между векторами AB−→ и AD−→ равен 120 градусам (поскольку 6 треугольников образуют шестиугольник), то cos(120°) = -0.5.
Подставляем известные значения в формулы:
AB−→⋅AD−→ = |AB−→|⋅|AD−→|⋅cos(120°) = 42 см⋅42 см⋅(-0.5) = -882 см².
Ответ: AB−→⋅AD−→ = -882 см².
2. Аналогично предыдущему случаю, для определения величины скалярного произведения OF−→ и OA−→ необходимо вычислить произведение их длин и умножить на косинус угла между ними.
Определение длины вектора OF−→: так как сторона треугольника равна 42 см, то длина вектора OF−→ равна длине стороны треугольника, то есть 42 см.
Длина вектора OA−→ также равна 42 см.
Угол между векторами OF−→ и OA−→ составляет 120 градусов (поскольку 6 треугольников образуют шестиугольник), поэтому cos(120°) = -0.5.
Применяем формулу для скалярного произведения:
OF−→⋅OA−→ = |OF−→|⋅|OA−→|⋅cos(120°) = 42 см⋅42 см⋅(-0.5) = -882 см².
Ответ: OF−→⋅OA−→ = -882 см².
3. Для нахождения скалярного произведения векторов CB−→ и CD−→ также нужно вычислить произведение их длин и умножить на косинус угла между ними.
Длина векторов CB−→ и CD−→ равна длине стороны треугольника, то есть 42 см.
Угол между векторами CB−→ и CD−→ также равен 120 градусов (поскольку 6 треугольников образуют шестиугольник), поэтому cos(120°) = -0.5.
Вычисляем скалярное произведение:
CB−→⋅CD−→ = |CB−→|⋅|CD−→|⋅cos(120°) = 42 см⋅42 см⋅(-0.5) = -882 см².
Ответ: CB−→⋅CD−→ = -882 см².