Дан параллелограмм со сторонами 10 и 14, и с углом 150◦ . Найдите площадь прямоугольника, полученного в результате взаимных пересечений биссектрис всех углов этого параллелограмма.
Другие вопросы по теме Геометрия
Популярные вопросы
- Определить относительную плотность метана (ch2)по воздуху...
1 - Маргулан купил 10 учебников. арман купил столько же. сколько всего учебников...
1 - Какие реформы провёл борис годунов....
2 - Выразите 4 мин 15 с в минутаз и запешите результат десятичной дробью...
2 - Что созревает на гаметофите а что на спорофите...
1 - Синформатикой ! 6 класс. надо вставить слова. нумеруйте их. пример: текст:...
2 - Сравните числа, результат запишите с знаков или -7/12 и -5/12; -3/8 и 3/10...
3 - )докажите тождество: 1)а+б-10аб=2а(3-б)-3б(а-2)-5(аб+а+б) ; 2) 4(2--m)-2(3m+4)=-17m-6....
2 - А. с. пушкин капитанская дочка гринев и швабрин....
3 - Что лучше когда в голове каша или ветер в голове...
3
4
Объяснение:
JCD - равнобедренный по двум углам
⇒ JD = DC = 10
⇒ KD = 4
JI = 10*sin(75°)
BK ║GD ⇒ ⇒ HI = 4*sin(75°)
⇒ HI = 4*sin(75°)
=====
BKA - равнобедренный по двум углам
⇒ AK = AB = 10
⇒ AJ = 4
KF = 10*cos(75°)
CJ ║GA ⇒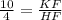 ⇒ FH = 4*cos(75°)
⇒ FH = 4*cos(75°)
====
S = 4*sin(75°) * 4*cos(75°) = 4
ꟷꟷꟷꟷꟷꟷ
Не забывайте сказать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!