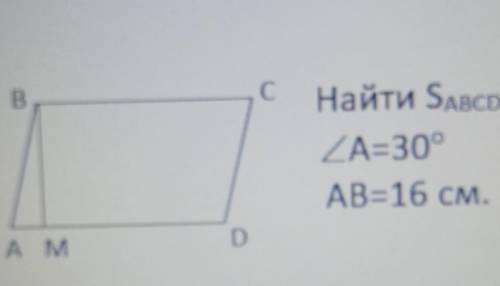
Дан параллелограмм с высотой BM найдите площадь этого параллелограмма ABCD если угол А равен 30 градусов а сторона AB 16 см

Для решения этой задачи, нам понадобится знание о параллелограммах и формулах для нахождения площади. Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны по длине. В данном случае, сторона AB имеет длину 16 см, и она параллельна стороне CD. Угол А равен 30 градусов, что означает, что угол В равен 150 градусов. Для нахождения площади параллелограмма, мы можем использовать формулу: Площадь = основание * высоту. В данной задаче у нас дана высота BM. Однако, чтобы вычислить площадь, нам нужно знать длину основания параллелограмма. К счастью, мы можем найти длину основания, используя теорему косинусов. 1. Найдем длину основания CD: Мы знаем, что сторона AB равна 16 см. Из теоремы косинусов, мы можем найти длину стороны CD: CD^2 = AB^2 + BM^2 - 2 * AB * BM * cos(A) Подставим известные значения: CD^2 = 16^2 + BM^2 - 2 * 16 * BM * cos(30) CD^2 = 256 + BM^2 - 32 * BM * cos(30) 2. Найдем длину стороны CD, вычислив квадратный корень из данного выражения: CD = √(256 + BM^2 - 32 * BM * cos(30)) 3. После того, как мы найдем длину стороны CD, мы можем вычислить площадь параллелограмма: Площадь = AB * BM Площадь = 16 * CD Таким образом, после нахождения длины стороны CD и зная длину AB, мы сможем вычислить площадь параллелограмма ABCD.