Дан параллелограмм ABCD. AD||BC,AB||CD. Треугольник ABF=4. Найти трапецию EFND= Ⓐ
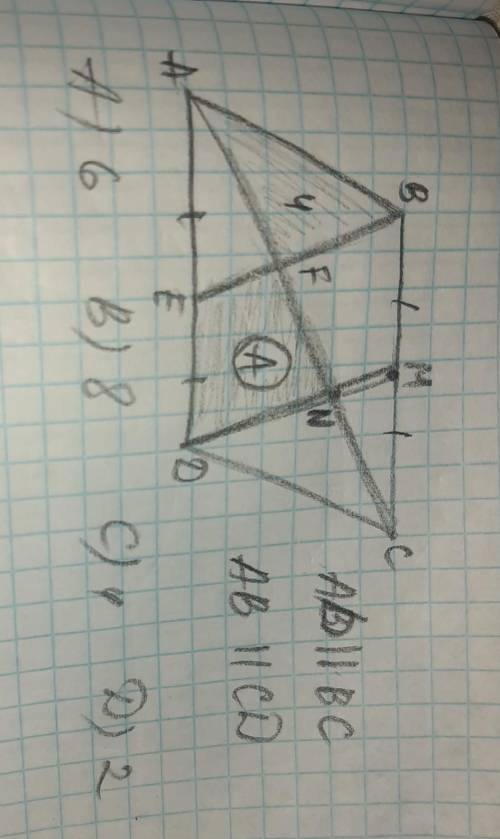
Другие вопросы по теме Геометрия
Популярные вопросы
- Разбор слова заросло по составу если есть однокоренные слова то напишите с ними...
3 - Complete the sentences using the words from the box between scary sack race were...
3 - Осуществите превращения: оксид кальция-карбид кальция-ацетилен-этаналь-этанол-этилен.напишите...
3 - Составить блок схему по : : бабушка попросила машу собрать ягоды крыжовника. девочка...
1 - 5. общая формула, соответствующая высшему оксиду 1)r20 2)ro 3)r203 4)r02 5) r205...
2 - Как пишется слова вовсе не убедительно,погостить недолго,невзначай,не так? почему?...
1 - Периметр прямоугольника 30см , его ширина 7 см. найди площадь прямоугольника ....
1 - До діжки з водою підведений шланг, через який у неї вливається 9 відер води за годину....
2 - Написать сообщение на тему быт и обычаи . !...
1 - Фонетический разбор слова розоватый...
2
4
Объяснение:
AC и BD - диагонали параллелограмма. По свойству диагоналей параллелограмма AC и BD пересекаются в одной точке и точкой пересечения делятся пополам. Проведем BD, пусть BD пересекает AC в точке O. Тогда BO = OD, получается, AO - медиана треугольника ABD.
BE - также медиана треугольника ABD. Медиана делит треугольник на два равновеликих треугольника. Тогда
S(ABE) = A(BED)
S(ABO) = S(ADO)
Из этого следует, что S(EFND) = S(ABF) = 4 (подробно см. рис)