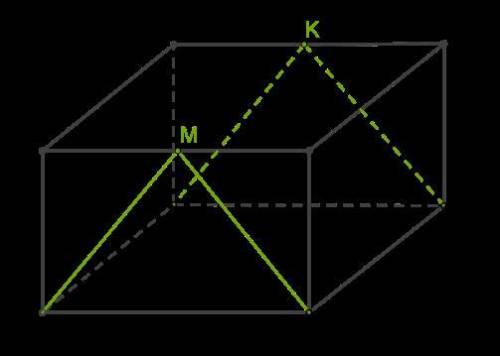
Дан параллелепипед ABCDA1B1C1D1. Точки M и K — середины рёбер A1D1 и B1C1 соответственно. Найди (вводи с латинской раскладки):
1. A1B1−→−− + A1M−→−− =
;
2. AA1−→− − D1A1−→−− =

Для начала, давай разберемся с обозначениями. Параллелепипед ABCDA1B1C1D1 - это тримерный объект, у которого есть вершины A, B, C, D, A1, B1, C1, D1.

Следующие обозначения важны для решения задачи:
- Мы знаем, что точки M и K это середины ребер A1D1 и B1C1 соответственно.

Теперь перейдем к решению задачи:

1. Найди вектор A1B1 - это вектор, который направлен от точки A1 к точке B1. Точки A1 и B1 имеют координаты (0,0,1) и (1,0,1) соответственно. Чтобы найти вектор A1B1, нам нужно вычесть координаты точки A1 из координат точки B1:
A1B1 = B1 - A1 = (1,0,1) - (0,0,1) = (1,0,0)

Далее, найдем вектор A1M - это вектор, который направлен от точки A1 к точке M. У нас уже есть координаты точек A1 (0,0,1) и M (0,1,1):
A1M = M - A1 = (0,1,1) - (0,0,1) = (0,1,0)

Теперь, чтобы найти сумму векторов A1B1 и A1M, нужно сложить их соответствующие координаты:
A1B1 + A1M = (1,0,0) + (0,1,0) = (1,1,0)

Ответ: A1B1 + A1M = (1,1,0)

2. Найди вектор AA1 - это вектор, который направлен от точки A к точке A1. Точки A и A1 имеют координаты (0,0,0) и (0,0,1) соответственно. Чтобы найти вектор AA1, нам нужно вычесть координаты точки A из координат точки A1:
AA1 = A1 - A = (0,0,1) - (0,0,0) = (0,0,1)

Далее, найдем вектор D1A1 - это вектор, который направлен от точки D1 к точке A1. У нас уже есть координаты точек D1 (1,1,1) и A1 (0,0,1):
D1A1 = A1 - D1 = (0,0,1) - (1,1,1) = (-1,-1,0)

Теперь, чтобы найти разность векторов AA1 и D1A1, нужно вычесть их соответствующие координаты:
AA1 - D1A1 = (0,0,1) - (-1,-1,0) = (1,1,1)

Ответ: AA1 - D1A1 = (1,1,1)

Надеюсь, что мое объяснение было понятно и подробное. Если у тебя еще есть вопросы, не стесняйся задавать!