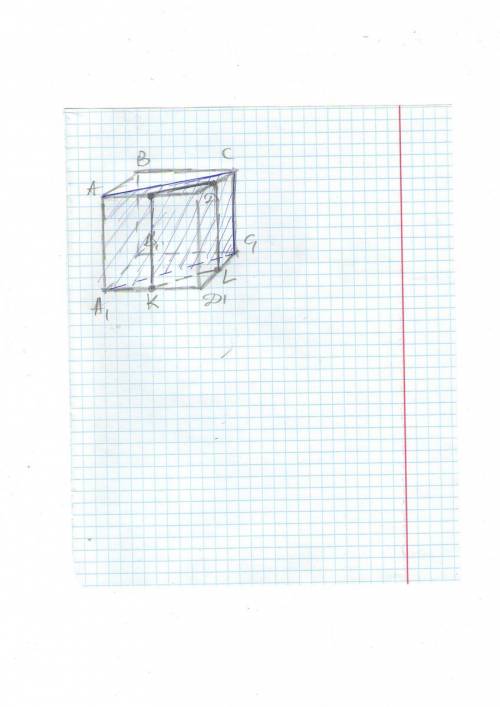
Дан куб авсdа1в1с1d. точки k, l, m, n–соответственно середины ребер a1d1, d1c1, dc, ad. докажите, что плоскость, которая проходит через эти точки, параллельна плоскости четырехугольника аа1с1с.
Ответы
Плоскости параллельны, если 2 пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости. Так что надо искать 2 прямые в одной плоскости и 2 прямые в другой плоскости. Если они попарно параллельны, то выполнится признак параллельности плоскостей.MN и ML - это пересекающиеся прямые (MNKL). АС и CC1 - это пересекающиеся прямые (А1АСС1). MN || AC ( средняя линияΔACD). MN || CC1 ( это рёбра куба). Признак параллельности выполняется. ( MNKL)|| (А1АСС1)
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Какой инструмент применяют для строгания? а. Шерхебель, рубанок;...
3 - Проведите морфемный разбор причастий и деепричастий Однажды в доме...
3 - Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20...
2 - Рівняння швидкості тіла v=2+4t. Яке рівняння відповідає залежності...
1 - Экологиялық мәселелер мен оның себептерін сәйкестендіріз...
3 - Умпа-лумпа у повісті чарлі і шоколадна фабрмка вмсміювали в своіх...
3 - До ть будь ласка В. Чемерис працює в редакції газети А. «Літературна...
1 - Решить уравнение. Уравнение на фото....
1 - Античная лирика, кратко и письменной....
3 - Закончи предложение: Я напишу по латышский потому что перевод может...
2