Дан куб abcda1b1c1d1 со стороной 5, точка o делит ac1 в отношении 1 к 4, считая от точки a. найти площадь поверхности общей части данного куба и куба, симметричного ему относительно точки o.

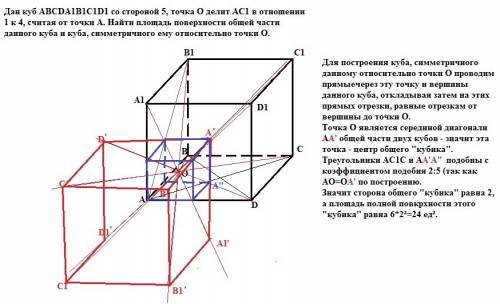
Для построения куба, симметричного данному относительно точки О проводим прямые через эту точку и вершины данного куба, откладывая затем на этих прямых отрезки, равные отрезкам от вершины до точки О и получаем вершину симметричного куба.Точка О является серединой диагонали АА' общей части двух кубов - значит эта точка - центр общего "кубика".  Треугольники АС1С и АA'A" подобны с коэффициентом подобия 2:5 (так как АО=ОА' по построению,  а АО:АС1=1:5 по условию).Значит сторона общего "кубика" равна 2, а площадь полной поверхности этого "кубика" равна 6*2²=24 ед².