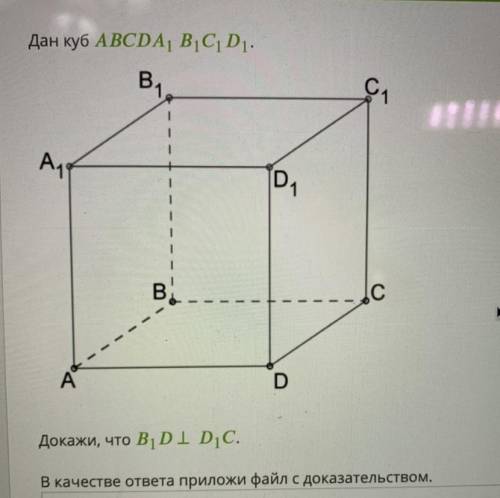
Дан куб ABCDA1B1C1D1. Докажите, что B1D перпендикулярна к D1C
Другие вопросы по теме Геометрия
Популярные вопросы
- Країна яка розширила права власних колоній вестмінстерським...
2 - Александр сергейовичь Пушкин капитанская дочка сумативная работа...
2 - Найти пример из фильма ,младший школьник объяснить с чем это...
2 - Лодка плывёт по реке, мальчик стоя в лодке стреляет из лука...
3 - Дан куб ABCDA1B1C1D1. Точка A2, - середина ребра AA1, Постройте...
3 - Объясните почему данные факторы послужили причинами бурного...
1 - Фокусна відстань збиральної лінзи 2 см. Предмет, висота якого...
1 - Наведіть 3 приклади хімічних явищ що відбуваються під час приготування...
3 - Два бильярдных шара одинаковой массы ,движутся на встречу друг...
3 - що впроваджує нового онєгін як поміщик...
1
Доказательство будет состоять из нескольких шагов.
Шаг 1: Покажем, что отрезок B1C1 параллелен отрезку AD.
Изображение куба нам дает следующую информацию:
- Основание ABCD является параллелограммом, так как противоположные стороны равны и параллельны.
- Основание A1B1C1D1 также является параллелограммом, так как противоположные стороны равны и параллельны.
- Линия B1C1 проходит через точку B1, которая является симметричной с точкой A относительно центра куба (O).
Из этих фактов следует, что отрезок B1C1 параллелен отрезку AD.
Шаг 2: Покажем, что отрезок B1D параллелен отрезку C1D1.
Изображение куба также нам даёт следующую информацию:
- Линия B1D проходит через точку B1 и точку D, которая является симметричной с точкой C1 относительно центра куба (O).
Из этого факта следует, что отрезок B1D параллелен отрезку C1D1.
Шаг 3: Покажем, что отрезки B1D и D1C перпендикулярны.
Мы уже установили, что отрезок B1D параллелен отрезку C1D1. Если две прямые линии параллельны, а третья линия перпендикулярна одной из них, то она также перпендикулярна и к другой прямой. Таким образом, поскольку B1D параллелен C1D1, а B1D перпендикулярна B1D (по построению), мы можем заключить, что B1D также перпендикулярна к D1C.
Таким образом, мы успешно доказали, что B1D перпендикулярна к D1C, используя свойства параллелограммов и факты о симметрии куба относительно его центра.