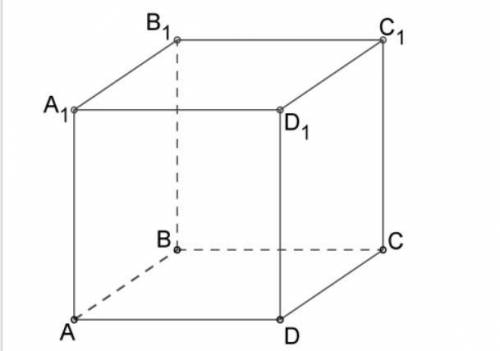
Дан куб ABCDA1B1C1D1. Докажи, что B1D⊥ D1C.

Для начала, мы можем взглянуть на данную фигуру и выделить все ее особенности.

Дан куб ABCDA1B1C1D1, что означает, что у нас есть 8 вершин (A, B, C, D, A1, B1, C1, D1) и 12 ребер, которые соединяют эти вершины.

Для доказательства того, что B1D ⊥ D1C, мы будем использовать определение перпендикулярности, которое гласит: если две линии перпендикулярны, то их углы между собой равны.

Обратим внимание на ребро B1D и ребро D1C. Для начала, рассмотрим проекции этих ребер на одну из плоскостей, например на плоскость ABCD.

Так как куб ABCDA1B1C1D1, то линии B1D и D1C лежат в плоскостях, образованных парами параллельных ребер, которые принадлежат плоскости ABCD. Таким образом, B1D и D1C лежат в плоскости ABCD и их проекции также лежат в этой плоскости.

Теперь, чтобы доказать перпендикулярность между B1D и D1C, мы должны доказать, что угол между их проекциями равен 90 градусам.

Для этого, мы можем рассмотреть ребра B1D и D1C. Обратим внимание, что при смотрении на фигуру с противоположной стороны (ответная сторона) к нам, ребра B1D и D1C расположены параллельно и пересекаются в точке D.

Теперь, если мы соединим точки B1 и D1 от вершин, которые лежат на сторонах ABCD, получим две линии, которые пересекаются в точке D1.

Таким образом, мы получили две точки пересечения (D и D1) и два параллельных ребра (B1D и D1C), что подтверждает перпендикулярность между ними.

Таким образом, доказано, что B1D ⊥ D1C.