1. Геометрия
  2. Дан четырехугольник с вершинами

Дан четырехугольник с вершинами А(3;5;4), В(4;6;5), С(6;-2;1) и D(5;-3;0). Является ли данный четырехугольник параллелограммом?

anna47983 anna47983    3   13.12.2020 22:38    0

Ответы
Dote8228 Dote8228  12.01.2021 22:38

Надо найти длину каждого отрезка. Это находиться за формулой(на картинке)

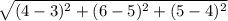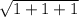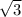
AB= \sqrt{(4-3)^{2}+(6-5)^{2}+(5-4)^{2} } = \sqrt{1+1+1} = \sqrt{3}

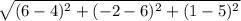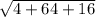BC= {\sqrt{(6-4)^{2}+(-2-6)^{2}+(1-5)^{2} } = \sqrt{4+64+16} = \sqrt{84}

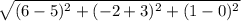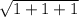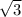
DC= {\sqrt{(6-5)^{2}+(-2+3)^{2}+(1-0)^{2} } = \sqrt{1+1+1} = \sqrt{3}

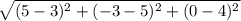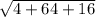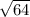
AD= {\sqrt{(5-3)^{2}+(-3-5)^{2}+(0-4)^{2} } = \sqrt{4+64+16}=\sqrt{64}

У параллелограммом противоположные стороны параллельны и равны, AB=DC, BC=AD, следовательно данный четырехугольник может быть параллелограммом


Дан четырехугольник с вершинами А(3;5;4), В(4;6;5), С(6;-2;1) и D(5;-3;0). Является ли данный четыре
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Galinachlen Galinachlen  03.05.2020 20:25
Найдите длину ортогональной проекции отрезка АВ на плоскость альфа, если АВ = а, а прямая АВ наклонена к плоскости альфа под углом 30 °​...
SaharaYo SaharaYo  03.05.2020 20:11
Найдите площадь кругового сегмента, если радиус окружности равен 5 см, а дуга содержит 30 °...
bondnm35 bondnm35  06.05.2021 07:15
AB диаметр BC хорда окружности угол АОС равно 110 градусов Найдите градусные меры углов треугольника ABC можно с чертежом аж надо​...
karolsevilla2017 karolsevilla2017  06.05.2021 07:16
И СДЕЛАЙТЕ КАК НАДО У МЕНЯ СОЧ ПО ГЕОМЕТРИИ...
Dasha142nikolaeva Dasha142nikolaeva  06.05.2021 07:17
Докажите, что треугольник авс с заданными точками a(-1; 1), b(1; 5), c (3; 1) равнобедренен :_(((​...
Зайченок157895 Зайченок157895  06.05.2021 07:17
Две прямые, проведённые из одной точки Е, касаются окружности с центром О и радиусом 14 см в точках С и К. Найдите угол между этими прямыми, если ОЕ=28см.​...
FOXI66666 FOXI66666  06.05.2021 07:19
Две окружности касаются внешним образом радиус одной в два раза больше радиуса другой найти диаметры этих окружностей псли расстояние между их центрами равно 15 см...
настя7073 настя7073  06.05.2021 07:19
В основі піраміди лежить прямокутний трикутник з катетом 12 см і гіпотенузою 20, см. Знайдіть об єм піраміди якщо всі її бічні ребра нахилені до площини під кутом...
Миша75040406 Миша75040406  12.08.2019 14:40
Найти координаты вектора 3 d еслиd {4; -2}...
the26 the26  12.08.2019 14:40
Втрапеции cdek из вершины d проведена прямая, параллельная боковой стороне ke до пересечения с большим основанием ck в точке n. периметр треугольника cdn=115см, а...

Популярные вопросы