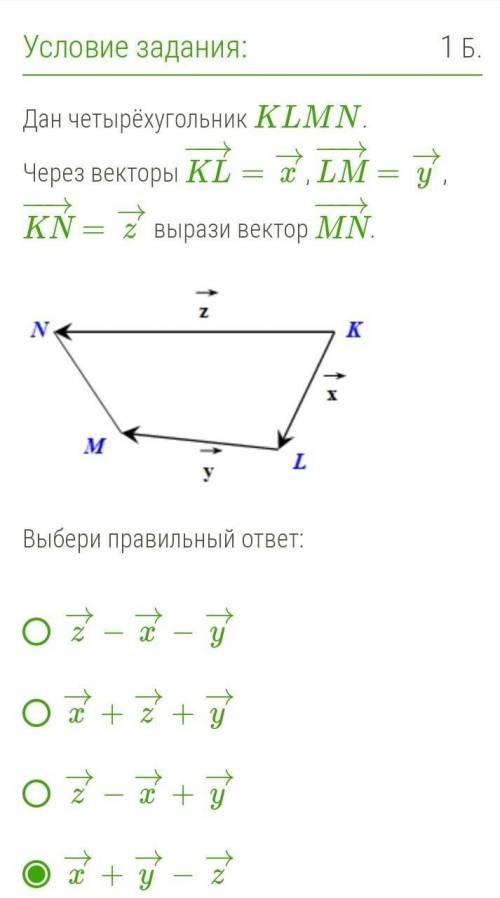
Дан четырёхугольник KLMN.
Через векторы KL−→−=x→, LM−→−=y→, KN−→−=z→ вырази вектор MN−→−
Другие вопросы по теме Геометрия
Популярные вопросы
- Отаршыл әкімшіліктіңойынша қазақ халқыныңбілім алуындасаяси тұрғыданЗиянды деп табылған...
3 - Постройте какой-нибудь параллелограмм, диагонали которого равны 6 см и 8 см....
1 - Аргумент из литературы на тему осторожность...
1 - Боковая сторона равнобокой трапеции равна 8см, а её диагональ делит среднюю линию...
3 - У завданнях 11-12 виберіть усі правильні варіанти відповідей. 11. Вкажіть властивості,...
2 - В данной природной зоне растет карликовая береза и ива. В таком лесу, говорят, грибы...
1 - Найди относительную молекулярную массу медьсодержащего вещества X: (На фото)...
3 - Аталады сұрағы сөз табыҚызыл сұрағы сөз табы Темір сұрағы сөз табы...
1 - Метанолу масою 18,8 г прореагувала з натрієм і виділився водень. Визначте об’єм...
2 - Установіть відповідність між зображенням комп ютерної графіки та об єктів...
2
Мы можем использовать два векторных уравнения, которые помогут нам выразить вектор MN−→ через данные векторы:
MN−→ = MK−→ + KN−→
MN−→ = KL−→ + LM−→ + MN−→
1. Векторное уравнение MN−→ = MK−→ + KN−→:
MN−→ = MK−→ + (KL−→ + LM−→)
MN−→ = MK−→ + KL−→ + LM−→
2. Векторное уравнение MN−→ = KL−→ + LM−→ + MN−→:
Перенесем MN−→ на другую сторону уравнения:
MN−→ - MN−→ = KL−→ + LM−→
0 = KL−→ + LM−→
Таким образом, мы получили два уравнения, которые помогут нам выразить вектор MN−→ через данные векторы:
MN−→ = MK−→ + KL−→ + LM−→
0 = KL−→ + LM−→
Теперь рассмотрим значение каждого вектора:
KL−→ = x→
LM−→ = y→
KN−→ = z→
Подставим данные значения в наши уравнения:
MN−→ = MK−→ + x→ + y→ (1)
0 = x→ + y→ (2)
Теперь мы можем решить систему уравнений (1) и (2) для определения вектора MN−→.
Для этого вычтем уравнение (2) из уравнения (1):
MN−→ - (x→ + y→) = MK−→ + x→ + y→ - (x→ + y→)
MN−→ - (x→ + y→) = MK−→
Теперь сложим x→ и y→, чтобы объединить их в один вектор:
MN−→ - (x→ + y→) = MK−→
MN−→ - (x→ + y→) = MK−→
MN−→ - (x→ + y→) = MK−→
Таким образом, мы выразили вектор MN−→ через данные векторы KL−→, LM−→ и KN−→:
MN−→ = MK−→ - (x→ + y→)
И это наше окончательное решение.