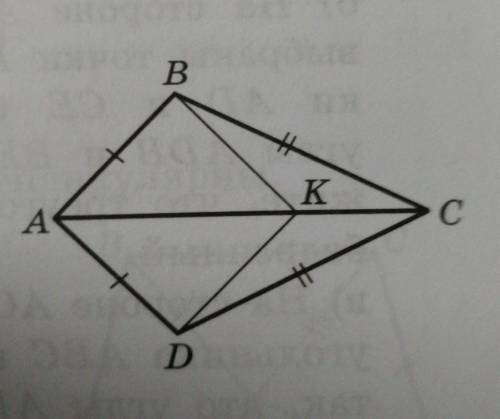
дан четырехугольник ABCD в котором AB=AD, BC=CD. На его диагонали AC взчли произвольную точку К. докажите что: 1) BK=DK 2) Угол BKD=углу DKC

Можно с объяснением?

Для доказательства утверждений 1) и 2), нам необходимо использовать свойства параллелограмма и свойства параллельных прямых. Параллелограмм - это четырехугольник, у которого противоположные стороны равны и параллельны.

1) Утверждение 1: BK = DK.

Для начала, обратим внимание на параллельные стороны треугольника BCD, это сторона BC и сторона CD. Параллельные стороны имеют равные длины.
Из этого следует, что угол BDC = углу BCD. (по свойству параллельных прямых).
Также, мы знаем, что AB = AD, и диагональ AC является общей для треугольников ABC и ADC.
Значит, треугольники ABC и ADC являются равнобедренными треугольниками.

Теперь, рассмотрим угол BAK и угол DAK.
Они соответственно являются углами при основании треугольников ABC и ADC. Так как треугольники равнобедренные, углы при основании также равны.
То есть, угол BAK = углу DAK. (углы при основании равнобедренного треугольника равны)

Теперь, рассмотрим треугольник BDK.
У него есть две равные стороны: BD и DK (по свойству параллелограмма).
Также, мы знаем, что угол BDK = углу ADM. (по свойству вертикальных углов)

Из равенства углов BAK и DAK, а также равенства углов BDK и ADM, мы можем заключить, что треугольники BDK и KDA равны по двум сторонам и одному углу (по стороне-уголу-стороне).
Следовательно, третья сторона треугольников, BK и DK, должны быть равны.

Таким образом, утверждение 1) BK = DK, доказано.

2) Утверждение 2: угол BKD = углу DKC.

Мы уже доказали, что треугольники BDK и KDA равны. Значит, и их углы также равны.
Так как угол BDK = углу ADM, следовательно, угол BKD = углу DKA.
А угол DKA = углу DKC, так как треугольники KDA и KDC также являются равнобедренными (аксиома равнобедренного треугольника).
Поэтому, угол BKD = углу DKC.

Таким образом, утверждение 2) угол BKD = углу DKC, доказано.

Результат:
1) Мы доказали, что в параллелограмме BK = DK.
2) Мы доказали, что угол BKD равен углу DKC.