Дан δавс равнобедренный, боковые стороны ab=bc. на стороне вс взяли точку d, при этом bd : dc = 1 : 3. нужно определить в каком отношении ad делит высоту bh δавс, считая от вершины в.
Другие вопросы по теме Геометрия
Популярные вопросы
- Решительно : из двух сел, расстояние между которыми 7 км , навстречу друг другу...
1 - Почему пала 2-я республика и оброзовалась 3...
1 - Может ли число 15a+78b где a и b некоторые натуральные числа,быть простымответ...
2 - Яприготовления бутылочного стекла берут 25 частей песка 9 частей соды и 5 частей...
3 - Задайте формулой линейную функцию,график которой параллелен прямой у=-3х+3 и...
3 - :файл размером 80 кбайт передаётся через некоторое соединение со скоростью 2048...
2 - Выполните действия: а) 3/5 * 2/7 * 5/6; б) 7/10 * 5/49 * 2/3...
2 - Какова с звязь между высотой гор и их окраской на карте?...
1 - Как вы считаете будет ли одинаковой скорость обращения 100 рублевых купюр и купюр...
1 - Написать сочинение на тему: кого можно назвать интеллигентным человеком?...
1
Пусть М — точка пересечения прямой AD и высоты BH. Через точку В проведём прямую, параллельную АС, и продолжим, AD до пересечения с это прямой в точке N. Пусть AH = CH = x, тогда AC = 2x.
Δ DBN ~ Δ CDA по двум углам, значит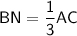
Также ΔAMH и ΔBMN подобны по двум углам. Из подобия мы имеем
ответ: 2 : 3.
ответ:Вот решение, как говорится, "на пальцах"
Объяснение: