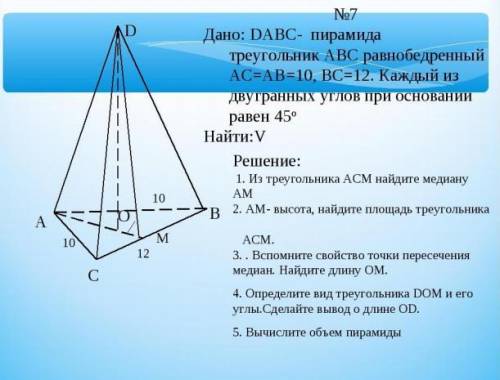
DABC- Пирамида треугольник ABC - равнобедренный AC=AB=10 СМ BC=12СМ
Каждый из двухгранных углов при основании равен 45 градусов
Найти V
Другие вопросы по теме Геометрия
Популярные вопросы
- АЙТЫЛЫМ 8-тапсырма. Қандай мамандық иесі болсаи я, туризммен хобби...
2 - Сочинение на тему вред и польза татуировок...
2 - Найдите стороны равнобедренного треугольника, если основание в три...
3 - У трикутнику ABC точка M- середина сторони BC, AC = 24 см Знайти...
3 - Переведите именнованый масштаб в численный. a)1 см.=300 м. b)1 см.=...
1 - Write a short poem about health 8 lines with rhyme(I m in 9th form...
2 - УМОЛЯЮ! НЕ ЖАЛЕЮ! ЗА ПОДРОБНОЕ РЕШЕНИЕ ОТВЕТ ПОСТАВЛЮ КАК ЛУЧШИЙ!...
2 - Б. Этот климатический пояс встречается только на непосредственных...
3 - О) 2. Два отрезка AB и CD пересекаются в точке 0 так, что АО = OB,...
2 - Определите график по формуле линейной функции. 1) y = 2x 2) y = 1,5x...
1
V = (1/3) * S * h,
где V - объем пирамиды, S - площадь основания пирамиды, h - высота пирамиды.
В данной задаче нам необходимо найти объем пирамиды DABC.
1. Первым шагом необходимо найти площадь основания пирамиды. Поскольку треугольник ABC является равнобедренным, то площадь треугольника можно найти по формуле:
S = (1/2) * a * b * sin(C),
где a и b - длины катетов треугольника, а C - угол между ними.
В нашем случае, a = AC = AB = 10 см, b = BC = 12 см, и угол C = 45 градусов.
S = (1/2) * 10 * 12 * sin(45) = 60 * sqrt(2) см^2.
2. Далее нам необходимо найти высоту пирамиды. Высота пирамиды проходит от вершины пирамиды до центра основания и перпендикулярна основанию.
Поскольку пирамида DABC является равнобедренной, то высота пирамиды будет являться медианой, проведенной из вершины пирамиды к основанию ABC.
Чтобы найти высоту пирамиды, мы можем использовать теорему Пифагора в треугольнике ABC.
Определим треугольник BAC. Так как треугольник ABC равнобедренный, то биссектриса угла между основанием и равными сторонами будет являться высотой.
Высота пирамиды будет равна высоте треугольника BAC.
По теореме Пифагора, катеты такого треугольника можно найти по формуле:
h^2 = a^2 - (b/2)^2,
где h - высота треугольника BAC, a - длина одного равного катета (AC или AB), b - длина основания BC.
В нашем случае, a = AC = AB = 10 см, b = BC = 12 см.
h^2 = 10^2 - (12/2)^2 = 100 - 36 = 64.
h = sqrt(64) = 8 см.
Таким образом, высота пирамиды DABC равна 8 см.
3. Теперь, имея площадь основания S = 60 * sqrt(2) см^2 и высоту пирамиды h = 8 см, мы можем найти объем пирамиды с помощью формулы:
V = (1/3) * S * h.
Подставим значения:
V = (1/3) * 60 * sqrt(2) * 8 = (1/3) * 480 * sqrt(2) = 160 * sqrt(2) см^3.
Таким образом, объем пирамиды DABC равен 160 * sqrt(2) см^3.