Діагоналі трапеції взаємно перпендикулярні. Одна з них дорівнює 6 см. Відрізок, що з'єднує середини основ трапеції, дорівнює 4,5 см і
проходить через точку перетину діагоналей. Знайдіть довжину другої
діагоналі.
Другие вопросы по теме Геометрия
Популярные вопросы
- Золото убило больше душ,чем железо тел. как понимать цитату ?...
3 - 2сосны растут на расстоянии 15 м одна от другой высота одной 130...
1 - На прогулке пёс шарик пробежал от дома до площадки 365 м ,от площадки...
1 - 6m+m-35=21 уравнение как решать и проверять...
1 - Скока будет ? 10000000000 - 9991 + 897 - 600 =...
2 - 50 , . сочинение на тему человек в 1 - 1,5 листа....
2 - Переведите числа из десятичной системы в двоичный, восьмеричную...
3 - Вычислите. 47*42+42*153 61*45+55*61 57*81-71*57 39*138-137*39...
1 - Нужно решить деление в столбик с остатком о . и повторяю это в...
2 - My cat lives in the forest. составить 3 вопроса...
2
Длина второй диагонали равна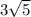
Объяснение:
Пусть диагональ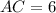 .
.
Треугольник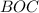 прямоугольный, причем точка
прямоугольный, причем точка 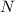 — середина гипотенузы
— середина гипотенузы 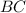 , поэтому
, поэтому 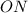 — медиана,
— медиана, 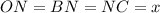 .
.
Аналогично в треугольнике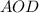
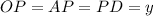 .
.
По условию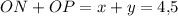 .
.
Продлим нижнее основание за точку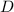 так, что
так, что 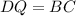 . Тогда
. Тогда 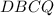 — параллелограмм,
— параллелограмм, 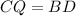 — вторая диагональ трапеции.
— вторая диагональ трапеции.
Так как угол между диагоналями прямой, то треугольник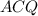 прямоугольный с катетом
прямоугольный с катетом 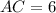 и гипотенузой
и гипотенузой
Тогда по теореме Пифагора