Діагоналі чотирикутника АВCD, вписаного в коло, перетинаються у точці М, а прямі АВ i CD перетинаються у точці N. Bідомо, що АMD=108°, AND=24°. Знайдіть кути А

66° и 42°

Объяснение:

Дано: Окр.О;

АВСD - вписанный четырехугольник;

АС ∩ BD = M; AB ∩ BC = N;

∠АMD = 108°; ∠AND = 24°.

Найти: ∠АBD и ∠BDC.

1.

Угол между пересекающимися хордами окружности равен полусумме двух противоположных дуг, высекаемых этими хордами.

⇒

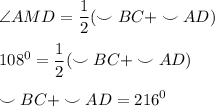(1)

Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.

⇒

(2)

Из (2) выразим дугу  AD и подставим в (1):

2. Теперь можем найти искомые углы.

Вписанный угол равен половине градусной меры дуги, на которую он опирается.

⇒