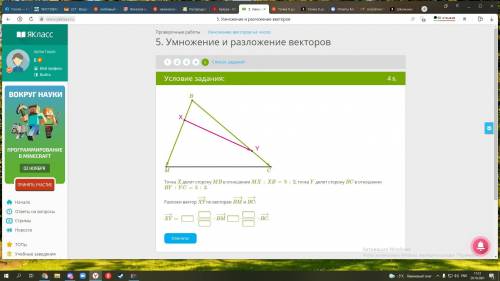
CРОЧНО Точка X делит сторону MB в отношении MX:XB=5:2, точка Y делит сторону BC в отношении BY:YC=5:2. Разложи вектор XY−→ по векторам BM−→− и BC−→−:
XY−→=
⋅BM−→−
⋅BC−→−.
Другие вопросы по теме Геометрия
Популярные вопросы
- разберите Задания для автоматически заполняемого кроссворда: Вычеркните лишнее...
1 - 11. В конструкторе два вида деталек разных цветов: кубики и цилиндры. Все цилиндры...
2 - Складіть і запишіть речененя, яке відповідало б такій характеристиці: питальне,...
1 - Кто в гарри поттере считал самой важной книгой тысячу волшебных растений и грибов...
1 - 3 задачи, как можно быстрее...
1 - Вважається, що Галицько-Волинське князівство стало спадкоємцем Русі-України ....
1 - Для представления 1 мин фильма на экране монитора с разрешением 1024 х 768 и палитрой...
3 - В каждом задании 1 ответ. 1.Каким членом предложения является выделенное имя существительное?...
1 - Программа python сделать скрин ім я файлу «завдання...
1 - Геометрія 7 клас трикутник описаний навколо кола , точки N , K ,P - точки дотику...
2
Для начала, мы можем выразить вектор MB−→ через векторы BM и MX:
MB−→=MX−→+XB−→
Теперь мы можем разложить вектор XY−→ по векторам BM−→− и BC−→−:
XY−→=XB−→+BY−→
Учитывая, что MX:XB=5:2 и BY:YC=5:2, мы можем записать XB−→ в виде:
XB−→=MX−→×(2/5)
Аналогично, мы можем записать BY−→ в виде:
BY−→=YC−→×(2/5)
Теперь мы можем подставить значения XB−→ и BY−→ в разложение XY−→:
XY−→=(MX−→×(2/5))+(YC−→×(2/5))
Для каждого слагаемого мы можем использовать конструкцию векторного произведения векторов:
(XY−→=(MX−→×(2/5))+(YC−→×(2/5)))=(MX−→×2/5)+(YC−→×2/5)
Получившееся выражение уже является ответом на задачу.
Таким образом, мы разложили вектор XY−→ по векторам BM−→− и BC−→−.