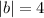Cоставить уравнение гиперболы , фокусы которой лежат на оси абсцисс симметрично относительно начала координат , если дана точка m(-5; 3) гиперболы и эксцентриситет е= sqrt 2 чему равна длина мнимой полуоси гиперболы
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. Проанализируйте стихотворение Д.С. Самойлова «Сороковые, роковые…». Не забудьте...
3 - Выделить границы деепричастным оборотом 1.Сад все больше радея и переходя в настоящий...
3 - 0,5 × |2х - 5| - 1 = 8 Уравление РЕШИТЕ...
2 - Составьте Фишбоун по сказке «Как один мужик двух генералов прокормил», взяв проблему,...
2 - Проверьте правильно или нет, если нет то скажите что....
1 - Маша, ученица 10 класса, купила в магазине косметичку на деньги, которые ей дали...
3 - Сообщение на тему дирижаблькак можно быстрее плз ...
1 - 1. Назвати вуглеводні та їх клас сH,C_H_C_H5 5 5 705...
3 - Надо ли ставить запятую в предложении К жаркой погоде мурка и вовсе вытягивается...
2 - Как человек использует водоросли пятый класс биология определение кратко...
1
Поскольку фокусы гиперболы лежат на оси абсцисс симметрично относительно начала координат, то это стандартная гипербола, которая имеет уравнение:
Поскольку дана точка гиперболы, то подставим ее координаты в уравнение:
Также распишем эксцентриситет гиперболы:
Преобразуем. Возведем в квадрат:
Подставим в уравнение с координатами выявленное соотношение:
Все необходимые данные для записи уравнения есть:
Поскольку квадрат мнимой полуоси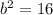 , то ее длина - соответственно
, то ее длина - соответственно