Цилиндр вписан в конус с образующей l= 5 см. Прямая, проведённая через центр верхнего основания цилиндра и любую точку окружности основания конуса, образует с основанием конуса угол в 45°. Угол образующей конуса с высотой конуса равен 30°. С точностью до сотых определи радиус цилиндра r.

Ответы

aniyzelenev 30.12.2020 12:33

1. Для определения r= O1C1 используем подобие треугольников ΔAPO∼ΔC1PO1.

2. Из треугольника APO:

PO=AP*cos30=l*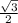 $\frac{ \sqrt{3} }{2}$

AO=AP*sin30=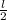 $\frac{l}{2}$

3.из треугольника AO1O

OO1=AO*th45=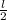 $\frac{l}{2}$

4.PO1=PO-OO1=l*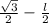 $\frac{\sqrt{3}}{2} -\frac{l}{2}$

5.трAPO подобен C1PO1

$\frac{PO}{PO1} =\frac{AO}{AO1} \\$

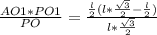r=C1O1= $\frac{AO1*PO1}{PO} = \frac{\frac{l}{2} (l*\frac{\sqrt{3}}{2}-\frac{l}{2} ) }{l*\frac{\sqrt{3}}{2} }$ = $\frac{l\sqrt{3}-l }{2\sqrt{3} } = \frac{5(\sqrt{3}-1)}{2\sqrt{3} } =1,06$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

nasty1512200229 04.09.2019 18:00

Найти sin альфа, если cos альфа = 0,8...

marichkakyhar 04.09.2019 18:00

Вравнобедренном треугольнике одна сторона меньше чем другая в 2 раза периметр 40 см найти стороны...

ilyuxayakovlev 04.09.2019 18:00

Биссектриса угла при основании равнобедренного треугольника равна 40 градусов найдите остальные углы...

Aegon 04.09.2019 18:00

В∆ abc угол c равен 90° , угол a равен 60° . ab-18см. найдите ac . ....

andryushaivcheoo 14.02.2020 08:36

В прямоугольном треугольнике один угол 60° разность гипотенузы и меньшего катета 3см Найдите гипотенузу и меньший катет...

BestPe 14.02.2020 08:41

В равнобедренном треугольнике одна сторона равна 7см вторая 10.Найдите 3 сторону ...

КейтKate 14.07.2019 01:30

Відповідні сторони подібних трикутників дорівнюють 14 см і 21 см. знайти площу ме- ншого трикутника, якщо площа більшого трикутника дорівнює 180 см2 ....

vorsunovakatv 14.07.2019 01:30

Утрикутнику авс ав = 3 см, ас = 2 см і ∠a = 30°. знайти довжину медіани вм...

mashadadihf 19.05.2020 12:53

При якому значенні x вектори с(3;9) та d(1; x) колінеарні? ...

пелы 19.05.2020 12:53

В треугольнике АВС АС=5√(3 ), ВС=4, угол А равен 60°. Найдите угол В....

Популярные вопросы