1. Геометрия
  2. Цилиндр описан около шара.Найдите

Цилиндр описан около шара.Найдите объём шара,если объём цилиндра 78​

Katerka Katerka    1   03.06.2021 11:52    5

Ответы
rasgramorysergio5775 rasgramorysergio5775  03.07.2021 12:54

Объём шара = 52

Объяснение:

Формула объёма шара:

V=\frac{4}{3}\pi R^{2}

Необходимо найти радиус шара.

У  шара и у цилиндра общий радиус. Основание цилиндра это круг с радиусом R, высота цилиндра равна двум радиусам. Значит объём цилиндра вычисляется по формуле:

V=\pi R^{2} *2R

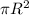где \pi R^{2} - площадь основания цилиндра,

2R - высота цилиндра

Подставим объём цилиндра = 78 из условия задачи в данную формулу, и выразим радиус:

78 = \pi R^{2} *2R\\\\ 78 = 2\pi R^{3} \\\\ R^{3} = \frac{33}{2\pi }

Оставим выражение в таком виде, выражать радиус (извлекать корень третьей степени) не обязательно, так как нам понадобится именно R³.

Таким образом, объём шара будет равен:

V=\frac{4}{3} \pi R^{3}=\frac{4}{3}\pi *\frac{78}{2\pi} = \frac{2*78}{3} = 52


Цилиндр описан около шара.Найдите объём шара,если объём цилиндра 78​
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
sinikyn1001 sinikyn1001  24.04.2020 20:23
решить самостоятельную работу. Завтра нужно здать...
Katyyyp Katyyyp  24.04.2020 20:22
В треугольнике абс угол с=60 градусо, угол б=90 градусов,ас 10см.найти бс...
DartMatv DartMatv  24.04.2020 20:22
В окружности хорды MN и PK пересекаются в точке O1. Известно, что MO1 = 4 см, NO1 = 8 см, PO1 : O1K = 1 : 2. Найдите PO1. ответ дайте в сантиметрах....
verakras verakras  24.04.2020 20:22
DO- висота, кут CDO= 70°, кут ODP=10°. Знайти кут C,D,P....
мейрбек2 мейрбек2  24.04.2020 20:22
Скласти рівняння з двома змінними за такою умовою: зошит коштує х грн., а ручка - у грн.; 2 ручки дорожчі за 5 зошитів на 1,2 грн....
123abcde6 123abcde6  24.04.2020 20:22
ОЧЕНЬ Высота BK прямоугольного треугольника ABC, опущенная на гипотенузу AC, разбивает его на два прямоугольных треугольника, периметры которых равны ABK= 16 и...
Evgenevgenevgen Evgenevgenevgen  07.12.2021 20:52
На рисунке 96 AC=AD, AB перпендикулярно CD. Докажите, что BC=BD и угол ACB= углу ADB...
rgn123 rgn123  07.12.2021 20:50
Найдите координаты векторов ef если е(4,12) f(-4 ,-10)...
shaihiev shaihiev  07.12.2021 20:50
В равнобедренном треугольнике АВС с основанием АС проведена медиана ВD Найдите градусные меры углов ВDА и АВС если внешний угол ВСК равен 120...
NastyKot15246 NastyKot15246  07.12.2021 20:50
Пункт 18,19,20. И с рисунком...

Популярные вопросы