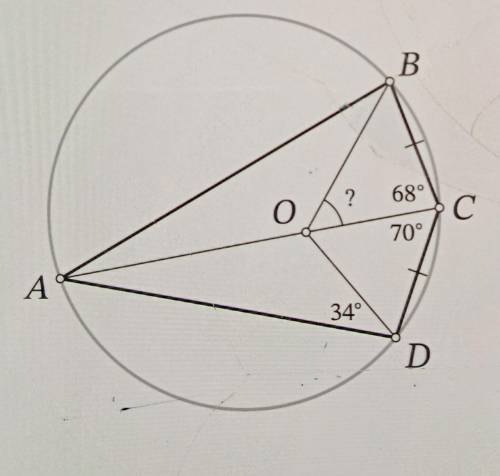
Четырёхугольник ABCD вписан в окружность. Известно что BC=CD, угол BCA=68° , угол ACD =70°. На отрезке AC отмечена точка O такая, что угол ADO =34°. Сколько градусов составляет угол BOC?
Другие вопросы по теме Геометрия
Популярные вопросы
- Дан треугольник со сторонами 3,5 см,4 см и 5 см. Большая сторона...
1 - Задания 1.Найдите значение выражения: (2,5-24) (-54+:(-5.6)...
2 - Опишите по пунктам как объединилась Франция...
1 - рочно Спишите данные предложения и обозначьте в них в соответствии...
2 - 1. Почему используются табличные процессоры? 2. В чем заключается...
1 - 4. На каком расстоянии друг от друга находятся два одинаковых...
2 - 9-тапсырма. Мәтіндегі ақпаратты «Төрт сөйлем» тәсілін пайдаланып...
3 - , не могу разобраться как найти S...
3 - Внимательно посмотрите на рисунок и занесите в таблицу меридианы...
3 - Мен жасаған жақсылық эссе 70 слов 3 абзац мақал-мәтел болу керек...
1
ABCD - вписанный, сумма противоположных углов 180.
∠BAD =180-BCD =180-68-70 =42
Равные хорды стягивают равные дуги.
BC=CD => ∠BAC=∠DAC (вписанные) =42/2 =21
∠COD =21+34 =55 (внешний угол △AOD)
∠CDO =180-70-55 =55
=> △OCD - р/б, CD=CO
=> CO=CB, △OCB - р/б
∠BOC =(180-68)/2 =56°