Через вершину прямого угла C треугольника ABC проведена прямая а перпендикулярно плоскости ABC. Плоскость, проходящая AB под углом 30° к плоскости ABC, пересекает прямую а в точке D. Найдите площадь треугольника ABD если AC=6дм, угол CAB=45°
Другие вопросы по теме Геометрия
Популярные вопросы
- Який об єм вуглекислого газу виділиться при бродінні глюкози 720г ? ответ...
1 - Зробити повний синтаксичний розбір речення співаю-і назустріч пісня ллється....
3 - Що змушувало хлопчика-зірку щоразу віддавати монету прокаженому? які душевні...
3 - Ctg(-x/2)=1, если не трудно можете дальше номер 146...
2 - Cрaвнитe прoцессы интeгрaции нa пoстсoвeтском прocтранстве с aнaлoгичными...
3 - 2+(-2)++(-2)=-12 не могу понять как решать...
1 - 43 только те, кто шарит, нужно сочинение с переводом....
2 - 2вопрос. 50 . только не с интернета....
3 - 15 ! найдите область определения каждого выражения...
3 - Найти сумму многочленов: 3x+1+-3x²-3x+1...
2
S=36дм^2
Объяснение:
Известны все углы треугольника ABC (C=90°; CAB=ABC=45°), известна сторона AC=6дм.
cosCAB=AC/AB; cos45°=6/AB; AB=6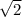 .
.
sinABC=BC/AB; sin45°=BC/6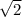 ; BC=6
; BC=6
Нашли стороны треугольника ABC, теперь найдем стороны ABD. В треугольнике BCD найдем гипотенузу B: cosDBC=BC/BD; cos45°=6/BD; BD=6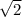 . По аналогии с треугольником BCD, ищем гипотенузу ACD; AD=6
. По аналогии с треугольником BCD, ищем гипотенузу ACD; AD=6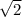 .
.
Формула площади прямоугольного треугольника: S=1/2*(ab);
S=1/2(6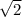 )^2=36дм^2
)^2=36дм^2