1. Геометрия
  2. Через вершину D прямокутника ABCD

Через вершину D прямокутника ABCD проведено пряму DK, перпендикулярну до його площини. KA = 5см; KB = 7см; KC = 6см.

Знайдіть:
а) KD
б) площу прямокутника ABCD

bititi2 bititi2    2   17.05.2020 01:31    5

Ответы
Masha6996 Masha6996  14.10.2020 20:59

(см. объяснение)

Объяснение:

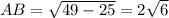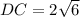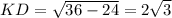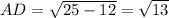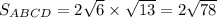По теореме о трех перпендикулярах ΔABK прямоугольный, откуда AB=\sqrt{49-25}=2\sqrt{6}. Тогда DC=2\sqrt{6}. Так как прямая DK перпендикулярна плоскости прямоугольника, то ΔCDK прямоугольный и => KD=\sqrt{36-24}=2\sqrt{3}см. Очевидно, что AD=\sqrt{25-12}=\sqrt{13}. Тогда S_{ABCD}=2\sqrt{6}\times\sqrt{13}=2\sqrt{78}см².


Через вершину D прямокутника ABCD проведено пряму DK, перпендикулярну до його площини. KA = 5см; KB
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
arzuvelieva arzuvelieva  29.07.2019 12:30
На боковых сторонах ab и bc равнобедренного треугольника abc отметили соответственно точки м и к такие,что bm=bk . докажите,что угол вак=углу всм...
rezeda231281 rezeda231281  29.07.2019 12:30
Точка o центр окружности, угол acb = 24 градуса . найдите величину угла aob...
usokolova071 usokolova071  06.02.2021 15:28
7 найдите неизвестный угол а) х:у =8:5...
NightyMigly NightyMigly  06.02.2021 15:30
1.Можно ли построить треугольник со сторонами: а) 5см,7см,12см; б) 11см,3см,9см; в) 4см,3см,8см. 2.В равнобедренном треугольнике стороны равны 4см и 7см. Какая из...
baktybaevalbina baktybaevalbina  06.02.2021 15:31
Блин сорри История:Написать сочинение на тему-что давало отвагу последнему хорезмшаху Джалолиддина Мангуберды?​...
karina200612 karina200612  06.02.2021 15:38
AM=x+4; MB=x; CM=5 x=? czy możesz wyjaśnić przebieg podjętej decyzji...
Elyzaveta2004 Elyzaveta2004  29.05.2020 01:48
Радіус основи прямого кругового конуса дорівнює 12 см, а твірна- 20 см. Знайти об єм та бічну поверхню конуса.​...
Kiberyblydok23 Kiberyblydok23  29.05.2020 01:48
3. Ребро куба збільшили в 2 рази. На скільки відсотків збільшиться: куба; А) поверхня Б) об єм куба?​...
lenusyamailru lenusyamailru  29.05.2020 01:41
Кр з геометрії 7 клас Кр з геометрії 7 клас...
0DinaLime0 0DinaLime0  29.05.2020 01:41
Маємо квадрат ABCD. Через кінцеву точку C діагоналі AC, що дорівнює 12,8 од. вим., проведено пряму перпендикулярно до діагоналі AC. Проведена пряма перетинає прямі...

Популярные вопросы