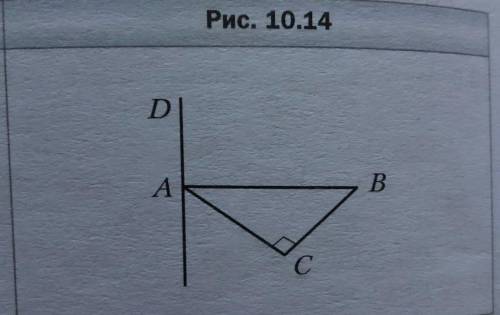
через вершину А прямоугольного треугольника ABC (ACB=90 градусов) проведённая прямая AD перпендикулярная плоскости ABC. Найдите расстояние между прямыми AD и BC если AB=10см BAC =45 градусам
Другие вопросы по теме Геометрия
Популярные вопросы
- У процесі фотосинтезу що описаний рівнянням реакції: 6nCO2+5nH2O- (C6H10O5)n +6nO2...
1 - 1 Про який жанр своїх творів О. Уайльд говорив Це прозові етюди, написані в романтичному...
1 - Преобразуйте в многочлен выражения: 1) 4m2n (-6mn2) 2) (-ab3)27a4 3) 5(a+3)(5-a)...
1 - Что такое осциллограф и его виды?...
3 - Для моллюска прудовика характерен следующий тип нервной системы: 1)сетчатая нервная...
3 - Какие два недостатка были осуждены современной критикой работы чарльза Диккенса...
3 - Рассматриваются четыре парных линейных регрессионных модели. Известны коэффициенты...
2 - Построи прямоугольные треугольники...
1 - дайте развёрнутый ответ на во Какое оно? О чем думали, о чем мечтали дети осажденного...
1 - Посмотри на картинку. Разделите эти бактерии на виды и напишите их названия....
1
Дано:
AB = 10 см - это длина стороны треугольника, обозначим ее как c (гипотенуза)
BAC = 45 градусов - это угол между сторонами AB и AC
Нам необходимо найти расстояние между прямыми AD и BC.
Шаг 1: Найдем длину стороны AC.
Для этого воспользуемся свойствами треугольника, в котором синус угла равен отношению противолежащей стороны к гипотенузе. Так как BAC = 45 градусов, мы можем использовать свойства прямоугольного треугольника со сторонами 10 см, AC и AB.
sin(BAC) = AC / AB
sin(45) = AC / 10
√2/2 = AC / 10
AC = 10 * √2 / 2
AC = 5√2 см
Шаг 2: Найдем угол между плоскостью ABC и прямой AD.
Угол BAC равен 45 градусов, и угол между AD и плоскостью ABC будет прямым, так как они перпендикулярны.
Шаг 3: Найдем длину отрезка CD.
Так как AD перпендикулярна плоскости ABC, отрезок CD будет являться высотой треугольника ABC. Так как AD проводится через вершину A, то CD будет служить основанием прямоугольного треугольника ACD.
Мы знаем, что площадь треугольника равна половине произведения его основания на высоту. В данном случае, площадь треугольника ABC равна половине произведения стороны AB на сторону AC.
Площадь треугольника ABC = (1/2) * AB * AC
= (1/2) * 10 * 5√2
= 25√2
Мы также знаем, что площадь треугольника ABC можно выразить как половину произведения одного его катета на гипотенузу: (1/2) * AC * BC.
Площадь треугольника ABC = (1/2) * AC * BC
25√2 = (1/2) * 5√2 * BC
Отсюда мы можем найти значение BC:
BC = (25√2) / (1/2 * 5√2)
BC = 50 / 5
BC = 10 см
Таким образом, расстояние между прямыми AD и BC равно 10 см.