Через вершину а прямоугольника abcd проведена прямая ак, перпендикулярная к его плоскости. известно, что kd = 6 см, kb = 7 см, kc = 9 см. найдите расстояние между прямыми ак и вc.

Нас просят найти расстояние между АК И BC. AB=3\sqrt[2]{5}

Объяснение:Из единственности перпендикуляра между скрещивающимися прямыми из рисунка понятно что это и есть прямая АВ.

По теореме о трех перпендикулярах Треугольник КВС прямоугольный и прямым углом является угол КВС и по теореме пифагора ВС равен 81-49=32 ,извлекаем из под корня и ВС равен 4.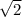

Также BC=AD

Из треугольника КАD по теореме пифагора получаем КА=2 и из треугольника КСА вычисляем диагональ прямоугольника АС=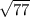

По теореме Пифагора вычитаем из квадрата АС квадрат BC