1. Геометрия
  2. Через точку м стороны ав треугольника

Через точку м стороны ав треугольника авс проведена прямая, перпендикулярная высоте bd и пересекающая сторону вс в точке р; вм=5 см, вр= 8 см, вс=24 см. а) найдите ab. б) найдите отношение площадей треугольников мрв и abc. распишите подробно !

Lizkic Lizkic    2   06.10.2019 09:31    29

Ответы
werffhuj werffhuj  09.10.2020 23:19

а) АВ = 15 см

б)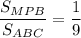 \dfrac{S_{MPB}}{S_{ABC}}=\dfrac{1}{9}

Объяснение:

BD⊥AC, так как BD высота,

BD⊥MP по условию, значит

АС║МР как перпендикуляры к одной прямой.

∠ВМР = ∠ВАС как соответственные при пересечении параллельных прямых МР и АС секущей АВ,

∠АВС общий для треугольников АВС и МВР, значит

ΔАВС ~ ΔMBP по двум углам.

а)

\dfrac{BM}{AB}=\dfrac{BP}{BC}

AB=\dfrac{BM\cdot BC}{BP}=\dfrac{5\cdot 24}{8}=15  см

б)

Площади подобных треугольников относятся как квадраты сходственных сторон:

\dfrac{S_{MPB}}{S_{ABC}}=\dfrac{BP^{2}}{BC^{2}}=\dfrac{8^{2}}{24^{2}}=\dfrac{1}{9}


Через точку м стороны ав треугольника авс проведена прямая, перпендикулярная высоте bd и пересекающа
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
TheSniper TheSniper  04.02.2021 15:54
1. Лист календаря частично закрыт предыдущим листом. Определи размеры листа календаря по следующим данным: �� = 1, �� = 4, �� = 3....
Naymchim Naymchim  04.02.2021 15:54
Ребро куба ABCDA1B1C1D1 дорівнює 2. Знайдіть відстань від точки O до вершин трикутника ABC, якщо точка O – центр грані A1B1C1D1. Відповідь округлiть до десятих....
Anzhelika35 Anzhelika35  04.02.2021 15:55
Як зміниться площа трикутника, якщо сторони, що утворюють кут a, зменшиться втричі, а кут a залишиться тим самим?...
vika5658 vika5658  04.02.2021 15:56
Отрезок AD биссектриса треугольника ABC. Через точку D проведенная прямая, параллельная стороне AB и пересекающая сторону AC в точке F . Найдите углы треугольника ADF, если...
vladshmko vladshmko  04.02.2021 15:56
Внешний угол ABC при вершине В равен 100°. Найдите градусные меры углов треугольника, не смежные с ним, если известно, что один из них на 400 больше другого с геометрией...
Finneas Finneas  04.02.2021 15:57
Дано: a||b . Параллельны ли а||с​...
Лина230502 Лина230502  04.02.2021 15:57
Дана величина угла вершины ∡ N равнобедренного треугольника RNM. Определи величины углов, прилежащих к основанию.  ∡ N= 115°; ∡ R= °; ∡ M= °. 2. Величина одного из прилежащих...
pbavaМАНЯ pbavaМАНЯ  04.02.2021 15:59
знайдіть кількість вершин правильного многокутника у якого зовнішній кут на 132° менший за внутрішній​...
Ihop Ihop  04.02.2021 15:59
В прямоугольном треугольнике АВС АС=5 см , ВС=5√3 см . Найдите угол В и гипотенузу АВ...
pepsy94zm pepsy94zm  04.02.2021 15:59
Із центра O квадрата ABCD проведено перпендикуляр SO (див. рисунок). Знайдіть ∠SCO, якщо AO=SO=7 см....

Популярные вопросы