Через точку А лежащую вне окружности проведены 2 секущие.Первая пересекает окружность в точках В и С,а вторая в точках М и N,так что АВ:АС=1:7 и АМ:AN=4:7. Найдите отношение ВС:МN.ответ запишите в виде целого числа или десятичной дроби
Другие вопросы по теме Геометрия
Популярные вопросы
- Каких людей о генрі називає справжніми волхвами...
3 - Закончил уравнение реакции, характеризующее химические свойства оснований, расставьте...
1 - Итоговый тест по русскому языку за курс 6 класса Вариант 1 1. В каком ряду во всех...
2 - Look and complete Saule wants to go to the beach by bus...
2 - Написать реферат на тему Проблема жизни и смерти, смысла и цели существования в...
3 - 14x + 5x = 608;53x - 26x = 1 863;x + 21x = 1 144:...
2 - составить предложения из слоа и словосочетаний: Переваривание, усвоение, то, что,...
2 - ЗАПИТАННЯ І ЗАВДАННЯ 1. Як впливає на природні компоненти господарська діяльність...
2 - Физика 7 класс на каз,языке ...
2 - ХЕЛП ОТ М’яч кинули вниз із висоти 1,5 м відносно підлоги. З якою швидкістю був...
2
(См. рисунок): пусть АВ = у, ВС = 6у, АМ = х, МN =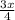 ; четырёхугольник ВСМN - вписанный ⇒ ∠1+∠3 = ∠2+∠4 = 180°. В ΔАВМ ∠АВМ = 180°- ∠2, ∠АМВ = 180° - ∠3 (как смежные углы) ⇒ ∠1 = ∠АМВ, ∠4 = ∠АВМ ⇒
; четырёхугольник ВСМN - вписанный ⇒ ∠1+∠3 = ∠2+∠4 = 180°. В ΔАВМ ∠АВМ = 180°- ∠2, ∠АМВ = 180° - ∠3 (как смежные углы) ⇒ ∠1 = ∠АМВ, ∠4 = ∠АВМ ⇒
ΔАВМ подобен ΔАСN (по трем углам, ∠А - общий) ⇒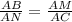
(AN = АМ + МN = x +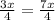 , AC = АВ + ВС = 7y) ⇒
, AC = АВ + ВС = 7y) ⇒ 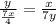 ⇒ 4y² = x² ⇒
⇒ 4y² = x² ⇒
x = 2y ⇒ MN =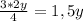 ⇒ ВС:МN = 6y : 1,5y = 4. ответ: ВС:МN = 4
⇒ ВС:МN = 6y : 1,5y = 4. ответ: ВС:МN = 4