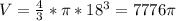Через конец радиуса шара проведено сечения, которое образует с радиусом шара угол 60°. найти объем шара , если площадь сечения равна 81π см^2.
Другие вопросы по теме Геометрия
Популярные вопросы
- Из группы туристов каждый приобрел памятные сувениры - но ни один...
2 - Нужно вставить пропущенные слова. Это синквейн. Казахский язык,...
2 - Большую Полоску бумаги разрезали на 4 части. После этого самую...
2 - Из пистолета при выстреле снаряд вылетел под углом 30° со скоростью...
2 - Номер параллелограмм, AM = CN....
2 - Познач рядок, в якому сполучення слів є словосполученням: впадає...
3 - Білге қаған - Шығыс Түрікқағанатыныңаумағынкеңейтіп,мемлекеттінығайтты.VII-VIII...
1 - Русский язык 7 класс стр 34 упр 52...
2 - Приставочный СуффиксальныйБессуффиксныйПриставочно-суффиксальныйпроверитьсиньлесникподоконникреть,...
1 - Что происходит с туловищем при старте куда устремлен взгляд?...
2
V=7776*π см³
Объяснение:
1. любое сечение шара плоскостью - круг.
по условию S=81π см²
S=πr²
πr²=81π, r²=81, r=9 см (r>0)
2. рассмотрим прямоугольный треугольник:
катет r =9 см - радиус круга - секущей плоскости
гипотенуза R - радиус шара
∠α =60° - угол между секущей плоскостью и радиусом шара, т.е между гипотенузой R и катетом r
∠β=90°-60°,
∠β=30° - угол между радиусом шара и перпендикуляром от центра шара до секущей плоскости
таким образом, радиус шара R=2 r, r -катет против угла 30°
R=18 см
3.