1. Геометрия
  2. Чему равняется отношение

Чему равняется отношение площи квадрата к площе вписаного в него круга?

airflash1372 airflash1372    2   10.03.2019 09:40    0

Ответы
egorywka egorywka  24.05.2020 15:52

Допустим сторона квадрата - а
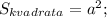
S_{kvadrata}=a^2;

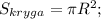
S_{kryga}=\pi R^2;

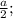
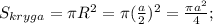
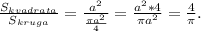
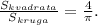
Так как круг вписан в квадрат, его радиус равен \frac{a}{2};

S_{kryga}=\pi R^2=\pi (\frac{a}{2})^2=\frac{\pi a^2}{4};

\frac{S_{kvadrata}}{S_{kruga}}=\frac{a^2}{\frac{\pi a^2}{4}}=\frac{a^2*4}{\pi a^2}=\frac{4}{\pi}.

ответ: \frac{S_{kvadrata}}{S_{kruga}}=\frac{4}{\pi}.

ПОКАЗАТЬ ОТВЕТЫ
eroly12ramblerr2 eroly12ramblerr2  24.05.2020 15:52

Решение:

Допустим сторона квадрата - а

Обоначим за стандарт сторону квадрата а,соответственно площадь квадрата равна а²,площадь круга равна πr²;
Знаем,что когда круг вписан в квадрат,тогда его радиус равен а/2:
Находим отношение площади квадрата к площади вписаного в него круга:


S(квадрата)= а²      =  а²*4  = 4

S(круга)          πа²/4     πа²      π


ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
nasten4ik0194 nasten4ik0194  18.09.2019 04:00
Втреугольнике abc точка d ∈ ab,a точка e ∈ bc так, что de//ac. в нем ab=42см db=14см be=23см. найти bc...
M89226691130 M89226691130  18.09.2019 04:00
Арифметическая прогрессия 1. даны члены арифметической прогрессии a2=7,16 и a3=9,35. вычисли разность прогрессии d= ? 2. вычисли 3-й член арифметической прогрессии, если известно,...
ledilove77 ledilove77  07.05.2021 05:04
1.(2)точка Д-середина отрезка КЕ.найдите координаты точки Е,если;К(3;2),Д(5;-2)...
vanyura vanyura  07.05.2021 05:00
От Люди . Решите полностью этот листок. (Спамеров ради я кидаю репорт, мне все равно вернутся )...
sellvladklim00oy13em sellvladklim00oy13em  07.05.2021 03:24
1.Через вершину С разностороннего треугольника АВС со стороной 2 см проведём перпендикуляр СД равной корню из 3см и к плоскости треугольника. Найти градусную меру двугранного...
1234567891248 1234567891248  01.06.2019 05:10
Найдите площадь кольца, ограниченного окружностями радиуса 3 см и 8 см. : )...
alyssasweetgirl alyssasweetgirl  01.06.2019 05:10
Решить 3 ! у меня уже есть дано , нужно только решение ! 1- дано : abcd ромб , ab=bc=dc=ad , ac=12 , sabcd=48 , найти bd ? 2- треугольник abc , урол a=75, угол с =75, ab =12 ....
Bayu1410 Bayu1410  21.10.2020 20:51
Вравнобедренный треугольник с основанием 12 си и высотой 8 см Вписан Квадрат так, что две еговершины лежат на основании треугольника, а даоставшиеся — на его боковых сторонах....
abogdanov94 abogdanov94  21.10.2020 20:51
Нарисуйте рисунок,с объяснением...
StepaBeng StepaBeng  16.10.2019 00:17
Номер 2.47 хотя бы часть с пояснениями...

Популярные вопросы