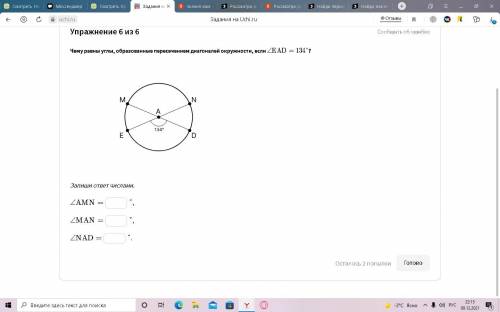
Чему равны углы, образованные пересечением диагоналей окружности, если ∠EAD=134° ?
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. Синтаксический разбор предложенияНа л..сных тр..пинках проваливася...
3 - Перечисли танцы, которые входят в Дивертисмент 2 действия балета «Щелкунчик»....
2 - Решите контррольную по обшесву там а1 и тд один во о ответ...
2 - Степень окисления центрального атома: KMnO4 Al2(SO3)3 Ca(OH)2...
2 - Розкласти на множника 9х^2у-36ху...
2 - Чи є правильним твердження: «Якщо один із суміжних кутів зменшити у...
2 - Какие системы участвуют в регуляции работы всех органов? 1.эндокринная...
3 - Електроплитка, ввімкнена в мережу з напругою 220В, чинить опір 22Ом....
1 - Що робити, якщо на тобі загорівся одяг?...
3 - Вычислите мощность нососа подающего ежеминутно 1,5м воды на высоту 20м...
2
ответ: <АMN=23°
<MAN=134°
<NAD=46°
Объяснение: За свойством углов между пересекающимися отрезками <EAD=<MAN, <NAD=<MAE
<NAD - смежный к углу ЕАD, значит равен 180-134=46°.
Отрезки МА и АN являются радиусом окружности, следовательно ∆MAN - равнобедренный с основанием MN, углы при основании равны. Отсюда, по свойству суммы углов треугольника <AMN=<MNA=(180-134):2=46:2=23°
Первое свойство, которое нам пригодится, гласит: "Диагонали, проведенные внутри окружности, делятся ими на равные части". То есть, если мы продолжим диагонали и соединим получившиеся точки, то получим два равных отрезка. Обозначим точку пересечения продолжений диагоналей как точку F.
Второе свойство, которое нам пригодится, гласит: "Если из центра окружности проведены лучи к точкам пересечения диагоналей, то эти лучи являются биссектрисами углов, образованных диагоналями". Обозначим центр окружности как точку O и соединим ее с точками пересечения диагоналей.
Углы, образованные пересечением диагоналей в окружности, будут равными в силу свойства процесса деления диагоналей внутри окружности. Другими словами, углы EAF и EDF будут равными, а также углы EBF и ECF будут равными.
Теперь давайте разберемся с данными из вопроса. У нас указан угол ∠EAD и нам нужно найти остальные углы.
Используя свойство биссектрисы, угол EAD будет равным половине суммы углов EAF и EDF. Поэтому, углы EAF и EDF будут равными по величине и будут составлять по 2/3 этой величины, то есть 2/3 * 134° = 89.33° каждый.
Теперь, используя свойство деления диагоналей, получаем, что углы EBF и ECF будут равными по величине и будут составлять 1/3 угла EAD, то есть 1/3 * 134° = 44.67° каждый.
Таким образом, углы, образованные пересечением диагоналей окружности, равны:
∠EAF = ∠EDF = 89.33°
∠EBF = ∠ECF = 44.67°
Надеюсь, это пошаговое объяснение поможет вам понять и решить задачу!