Чему равны стороны прямоугольника, если его периметр 74 дм, а площадь 3 м2?
Другие вопросы по теме Геометрия
Популярные вопросы
- Определи результирующую силу....
3 - Какой процесс называется рекомбинацей?...
2 - З літака, що летить горизонтально зі швидкістю 360 км/год на висоті 2 км...
1 - Каплю воды с эвгленами зелеными осветили фонариком справа. 1) Какое биологическое...
3 - Реакція між речовинами А та Б протікає по схемі: А+2В=С Концентрація речовини...
1 - Найдите значение дискриминанта 2х - х^2 = - 3...
2 - Задание № 4 1.Напишите письменную работу (объем 100 - 120 слов), сравнивая...
2 - с тестом по русскому языку ...
1 - Найдите множество значений а при котором уравнение 4x^2- 8x + a = 0 не имеет...
3 - 1. Кто был основателем Казахского ханства? 2. От какого хана откочевали...
1
Пусть стороны прямоугольника x и y. Учитывая, что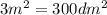 , получим систему уравнений:
, получим систему уравнений: