Центр окружности лежит на большем основании трапеции равно 20. найдите площадь этой трапеции если меньшее основание составляет 60% от большего.
Ответы
Назовем трапецию ABCD начиная с левого края большего основания, двигаясь по часовой стрелке.Так как центр окружности лежит на большем основании, это значит, что трапеция равнобедренная => большее основание является диаметром окружности. Проведем GO перпендикулярно AD. Получим угол AGD=90 градусов, как угол опирающийся на диаметр. Рассмотрим треугольник AGD -прямоугольный. Пусть AG=x,тогда и GD=x. По теореме Пифагора: 400=2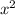 => х=10
=> х=10 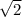 . Рассмотрим треугольник AGO - прямоугольный. По теореме Пифагора: GO =10. GO равно высоте трапеции. Получаем S=(BC+AD)GO/2= (0,6*20+20)*10/2=160
. Рассмотрим треугольник AGO - прямоугольный. По теореме Пифагора: GO =10. GO равно высоте трапеции. Получаем S=(BC+AD)GO/2= (0,6*20+20)*10/2=160
ПОКАЗАТЬ ОТВЕТЫ
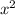 => х=10
=> х=10 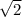 . Рассмотрим треугольник AGO - прямоугольный. По теореме Пифагора: GO =10. GO равно высоте трапеции. Получаем S=(BC+AD)GO/2= (0,6*20+20)*10/2=160
. Рассмотрим треугольник AGO - прямоугольный. По теореме Пифагора: GO =10. GO равно высоте трапеции. Получаем S=(BC+AD)GO/2= (0,6*20+20)*10/2=160
Другие вопросы по теме Геометрия
Популярные вопросы
- Слабораторной работе по программированию c++...
2 - Нужно решить интегралы ! заранее 1. x*dx/sqrt(3-4x^2) заменой переменных...
2 - Если к задуманому числу дописать с права 0, а потом из числа 143 вычесть...
1 - До санаторію завезли апельсини, мандарини та лимони. маса апельсинів...
2 - Как влияет увеличение числа проволок в кабеле (при их неизменном диаметре)...
3 - Площадь основания куба равна 8 см^2. найдите диагональ куба. найдите...
3 - Решите это правильно(обязательно), нужно до 28.06.19.как можно больше...
3 - Языквариант 3.1) вставьте пропущенные буквы и знаки препинания.(1) тихий...
2 - Покрасьте клетки доски 5×5 в пять цветов так, чтобы в каждом горизонтальном...
2 - Hi ! my name s johny atkins . i lake перевод...
1