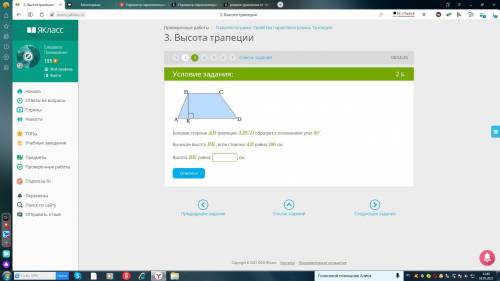
Боковая сторона AB трапеции ABCD образует с основанием угол 30°. Вычисли высоту BK, если сторона AB равна 100 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Test Open the brackets using Conditional I - Пишемо речення повністю.1 Peter (eat)...
1 - А) Скласти рівняння дотичної і нормалі до кривих у заданих точках: b). Скласти рівняння...
3 - Чому корозійна стійкість металів однозначно не пов язана з їхньою хімічною активністю....
3 - У якому з поданих варіантів, де сторони чотирикутника наведені послідовно, можливо...
1 - Исправьте ошибки в тексте.) Зимой 1237 г., после разгрома Индии, Мамай повел свои...
1 - Название климотические пояса, в которых расположен океан...
3 - Яку килькисть теплоти потрибно затратити, щоб розплавити 13,6 кг лоду, узятого за...
1 - . Прочитайте звернення принца Джона до «Лицаря, позбавленого спад- ку» (розділ IX)....
1 - 6. Розв яжіть рівняння х(2-x)+ х = 4. А4 Б 0,5 В-2 Г2...
1 - ЧТО ПОЛУЧИЛА И ЧТО ПОТЕРЯЛА ФРАНЦИЯ И АНГЛИЯ ПОСЛЕ СТОЛЕТНЕЙ ВОЙНЫ Франция: Англия:...
1
У нас есть трапеция ABCD, где AB - основание, а BC и AD - боковые стороны, которые мы обозначим как a и b.
Мы также знаем, что боковая сторона AB образует с основанием угол 30°.
Для начала, давай найдем угол BAD (α). Вспомним, что сумма углов треугольника равна 180°. Так как угол B равен 30°, то угол BAD будет равен 180° - 90° - 30° = 60°.
Теперь, обратимся к прямоугольному треугольнику ABK. Угол AKB (β) также равен 60° (потому что угол ABD равен углу B равен 30°).
Высота BK является противоположным катетом к углу β в прямоугольном треугольнике ABK.
Теперь, чтобы найти высоту BK, нам нужно использовать тригонометрическую функцию тангенса (тангенс β = противоположный катет/прилежащий катет). В данном случае, противоположный катет - это высота BK, а прилежащий катет - это сторона AB, которая равна 100 см.
Таким образом, у нас есть тангенс 60° = BK/100.
Для решения уравнения, выразим высоту BK: BK = 100 * тангенс 60°.
Тангенс 60° равен √3.
Теперь, подставим этот числовой ответ в наше уравнение:
BK = 100 * √3 ≈ 173.21 см.
Таким образом, высота BK равна примерно 173.21 см.
Вот и все! Надеюсь, это объяснение помогло тебе понять, как мы получили ответ. Если у тебя есть еще какие-либо вопросы, не стесняйся задать их!