Биссектрисы углов B и C треугольника ABC пересекаются в точке K. Найдите < ВКС, если < В = 28˚, а < С = 84 ˚.

Тогда с теоремы о сумме углов треугольника:

∠A + ∠B + ∠C = 180˚ ⇒

∠A = 180˚ - ∠B - ∠C = 180˚ - 28˚ - 84˚ = 68˚.

Так, как BS и CR - биссектрисы, то они делят:

∠B и ∠C пополам, из этого:

∠SBC = =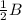

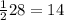
∠RCB = =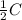

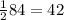
Тогда, с теоремы, о сумме углов треугольника:

∠SBC + ∠RCB + ∠ВКС = 180˚ ⇒

∠ВКС = 180˚ - ∠SBC - ∠RCB =  180˚ - 14˚ - 42˚ = 124˚.

ответ: 124˚.

Рисунок: